Dostaję dosyć dużo pytań odnośnie wprowadzonego przeze mnie w Kursie Całek Nieoznaczonych wzoru na postać kanoniczną funkcji kwadratowej.
Wzór:
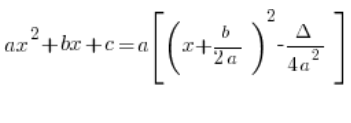
pojawia się w schemacie na rozwiązywanie całek wymiernych w Lekcji 5 Kursu:
Dlaczego tam jest a^2?
Problem jest taki, że na pierwszy rzut oka różni się on od postaci kanonicznej znanej ze szkoły średniej:
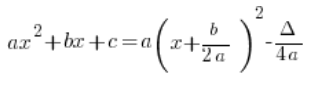
Standardowym pytaniem tutaj jest: „Czemu u Pana jest tam 
w mianowniku?”
Przekształcenie wzoru
Wystarczy jednak zauważyć, że jeśli we wzorze:
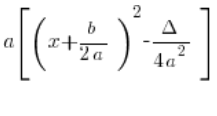
Przemnożymy 
przez nawias kwadratowy otrzymamy dokładnie wzór:
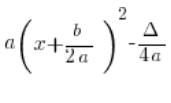
(po przemnożeniu przez składnik 
się skróci i wyjdziemy na 
)
Zatem obie te postaci są równoważne, czyli po prostu:
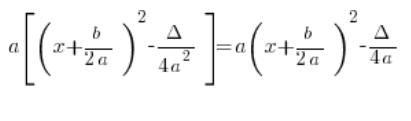
Po co więc wprowadzać ten wzór z nawiasem kwadratowym i a wyciągniętym przed nawias? Bo w całkach wymiernych tak jest wygodniej 🙂
W dalszych etapach liczenia całki i tak wykopać trzeba będzie przed znak całki (a najpierw przed nawias w mianowniku), na co więc czekać? 🙂
