Przy liczeniu pierwiastków drugiego stopnia w postaci kartezjańskiej (albo: algebraicznej) w moim Kursie Liczb Zespolonych pokazałem pewien patent, polegający na dopisaniu trzeciego równania do układu już dwóch istniejących, co w rezultacie gigantycznie skracało i upraszczało dalsze obliczenia.
Patent pokazałem, ale w żaden sposób nie uzasadniłem.
No i właśnie na tą okazję otrzymałem ostatnio maila o treści:
Witam
Czy mógłby Pan wyjaśnić dlaczego możemy użyć patentu na dodanie trzeciego równania podczas obliczania pierwiastka drugiego stopnia z liczby zespolonej?
x^2 + y^2 = moduł liczby której pierwiastek mamy obliczyć
Jest to BARDZO dobre pytanie i naprawdę błogosławieni w matematyce Ci, którzy nie wierzą profesorom na słowo, tylko cały czas pytają: „A skąd to się wzięło?” 🙂
Uzasadnienie
No to nie pozostało mi już nic, tylko uzasadnić ten patent na jeden z możliwych sposobów:
Po kilku pierwszych złożeniach w obliczaniu pierwiastka mamy sytuację:
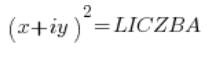
Skoro liczby (nie będę już za każdym razem pisał: „liczby zespolone”) po lewej i po prawej są równe, to ich moduły też muszą być równe (w drugą stronę to nie zachodzi, ale to nieważne), czyli:
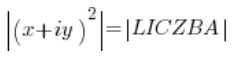
liczba do kwadratu to jest liczba razy liczba, czyli:
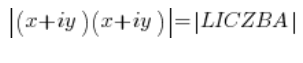
Moduł liczby zespolonej ma własność: ![]() , czyli po lewej stronie możemy zapisać:
, czyli po lewej stronie możemy zapisać:
![]()
…no i licząc moduły po lewej mamy:
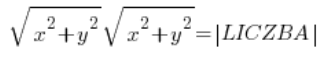
czyli:
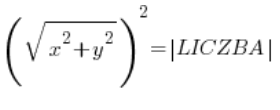
czyli:
![]()
czyli:
BINGO
Dzięki za dobre pytanie!



4 Komentarzy
Mateusz
Witam. W tym wspaniałym dniu życzę Panu wszystkiego co najlepsze. Dużo zdrówka i dalszej motywacji do tego, aby nadal powstawały kolejne wspaniałe kursy i pojawiały się na tej stronie. Tutaj zawsze chętnie wracam:)
Pozdrawiam
Krystian Karczyński
Już po Świętach, ale bardzo dziękuję i pozdrawiam!
Mateusz
Zastosowałem w zeszłym roku ten patencik na zajęciach z liczb zespolonych. Profesor oczywiście znał ten myk ale wcześniej nam tego nie pokazał. Podzieliłem się z tym patentem z całą grupą. To bardzo dobry sposób jest. Profesorowi się to podobało. Myk na szybkie obliczenia pierwiastka np. z liczby minus 16 też przedstawiłem na tych zajęciach. Pozdrawiam
Krystian Karczyński
Masz dobrego profesora, często nauczający źle reagują na takie patenty.
Zresztą pamiętam, jak zaczynałem korepetycje, przez dobre kilka lat miałem coś takiego: uczniowie pokazywali mi jakieś wyniesione z zajęć patenty, czy sposoby – a ja i tak na upartego chciałem nauczyć ich „po swojemu” 🙂