Ogólna instrukcja wpisywania formuł matematycznych
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Gdy przychodzi do korzystania z wielu matematycznych narzędzi (takich jak np. kalkulatory ONLINE) powstaje nam wcale niemały problem, jak napisać takie coś…
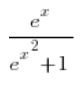
…”żeby komputer zrozumiał”. Czyli nauczenie się wpisywania formuł i wzorów matematycznych z klawiatury komputera.
Nie jest to ani łatwe, ani przyjemne. Nie nastawiajmy się na szybkie sukcesy, a raczej przygotujmy do sporej dawki frustracji, zwłaszcza przy starcie z bardziej złożonymi wyrażeniami.
Podstawowe działania
Zaczynamy od rzeczy prostych. Podstawowe operacje matematyczne oznaczamy jako:
+ dodawanie
– odejmowanie
* mnożenie
/ dzielenie
^ potęgowanie
Chcąc więc zapisać wyrażenie: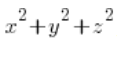 
, wpisał bym w kalkulator:
x^2+y^2+z^2
A jeśli miałbym do wpisania: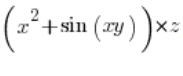 
, wpisał bym:
(x^2+sin(xy))*z
Wyrażenia bardziej skomplikowane
Trudniej nam się robi, gdy nasze wyrażenie jest jakby bardziej skomplikowane. Weźmy: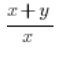 
Jeśli wpiszemy tą formułę “z palca”, jak leci, czyli:
x+y/x
Kalkulator “zrozumie” ją jako: 
, co jest nawet logiczne, bo mądrala zna kolejność działań (najpierw dzielenie, później dodawanie). Trzeba więc samemu wykombinować, żeby cały licznik wziąść w nawias przy wpisywaniu w kalkutor:
(x+y)/x
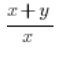
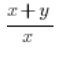
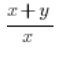
…choć przecież na wejściu: tego nawiasu nie było.
Co do pierwiastków: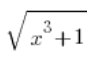 
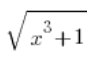
wpiszemy jako:
sqrt(x^3+1) , albo jako: (x^3+1)^(1/2) (bo ze średniej pamiętamy, jak to z tymi wykładnikami ułamkowymi było)
Na i na razie chyba tyle, bardzo proszę, zadawajcie pytania w komentarzach i wpisujcie tam wyrażenia, których nie umiecie wpisać poprawnie – będę pomagał i zrobi się z tego z czasem fajny materiał.
No i najważniejsze – NIE PRZEJMUJCIE SIĘ, że idzie to ciężko na początku. Gra jest warta świeczki – a gramy o dostęp do bardziej nowoczesnych matematycznych narzędzi niż kartka papieru i długopis. One naprawdę ułatwiają życie. Wyobraź sobie, że kiedyś w pracy musisz policzyć 10 całek potrójnych – ile czasu zajmie Ci to ręcznym tłuczeniem, a ile kalkulatorem?
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Tentukan turunan pertama dari fungsi berikut
F(x) =1/2×+3
Chce obliczyć logarytm o podstawie 2 z wartości bezwzględnej (x-3), w tym celu wpisuję komendę: log_(2)(|x-3|), co jest widziane przez program jako log_(2)(x)(|x-3|). Co zrobić by program widział to jako logarytm z |x-3| a nie z x*|x-3|?
Chodzi o WolframAlpha? Niech Pan wpisze: log_2|x-3|. U mnie działa:
https://www.wolframalpha.com/input/?i=log_2%7Cx-3%7C
Dzień Dobry.
Jak w kalkulatorze pochodnych cząstkowych wpisać funkcję z 4 zmiennymi, jakim symbolem oznaczyć czwartą zmienną ?
Witam,
jak obliczyc równianie różniczkowe y′+y^2⋅sinx=0 ?
Pozdrawiam i proszę o pomoc.
Jak wpisać wartość bezwzględną ?
Po prostu z klawiatury: |…|
Można też użyć funkcji ‘abs’, na przykład: abs(x-1)
Witam,
Jak obliczyć taką granicę funkcji zmierzającą do nieskończoności (2n+5)/sqrt(n^2+n+1) ?
Witam jak wprowadzić pierwiastek 3 stopnia?
Najlepiej będzie wpisać: sqrt(…)^(1/3) 🙂
Czy można wprowadzić pochodną po \lambda?
Najlepiej będzie wpisać funkcję w kalkulator ze zmienioną literką (np. zamiast lambdy wpisać “z” lub dowolną inną). I wtedy, w zależności od kalkulatora można wybrać opcje:
a) Wpisać cały wzór funkcji wielu zmiennych. Wyskoczą wszystkie proponowane pochodne i wśród nich wybrać tą odpowiednią (np
)
b) wpisać wprost, że potrzebna jest pochodna po konkretnej zmiennej, np “dx (FUNKCJA)”
Jak zapisać granice całki?
Jeśli chodzi np o WolframAlphe, to najlepiej jest posłużyć się formułą:
“integrate((WYRAŻENIE),DOLNA GRANICA CAŁKOWANIA, GÓRNA GRANICA CAŁKOWANIA) ”
Taka uwaga, słówko “integrate” można również skrócić i wpisać zwykłe “int”, też pójdzie jako całka.
Czyli np. ” \int ((2x^3), 0, 7) “
Innym sposobem zapisania granic jest np: “integrate (WYRAŻENIE) from …DOLNA GRANICA.. to ..GÓRNA GRANICA..”
Np. ” \int (2x^3) from 0 to 7 “
Jak wprowadzić liczby zespolone?
A co dokładnie potrzebujesz wprowadzić? 🙂
Jak wyznaczyć dziedzinę funkcji:
(x)= licznik pod pierwiastkiem -x^2+2x+15/w mianowniku In(7x -4)
Dziedzina tej funkcji została wyznaczona w tym przykładzie:
jak wprowadzić log o podstawie 1/2 z (x^2)
log_(1/2)(x^2)
tangens hiperboliczny:)
Witam a w jaki sposób mam zapisać takie wyrażenie: ln(x+ √1-3x^2) +e^((x-2)/(3-x)) tam gdzie jest pierwiastek to tyczy się całego wyrażenia (1-3x^2)
to będzie: ln(x+(1-3*(x)^2)^(1/2))+e^((x-2)/(3-x)) 😉
Skoro jest to również dla całek niewłaściwych to jak zapisać nieskończoność?
Np. wpisać dwa razy literkę małe o, czyli:
oo
Albo angielski wyraz ‘infinity’
“cały licznik wziąść w nawias ”
nic nie trzeba ‘braść’, wystarczy “wziąĆ” 🙂
Witam jak wprowadzic lim x-> 0 ?
Np. tak: lim_(x->0)
jak wprowadzić ln x?
Normalnie: ‘lnx’. A co, nie wchodzi gdzieś?
wpisując lnx program uznaje to jako logarytm dziesiętny ( tak mi się wydaje bo wpisując: x^y*lnx program pokazuje (x^y log(x)
Akurat WolframAlpha tak ma już zakodowane, że logarytm naturalny wyświetla jako log(x) (czyli po naszemu jakby logarytm dziesiętny).
Aby wprowadzić do kalkulatora logarytm dziesiętny, trzeba wyjątkowo wyraźnie tą podstawę napisać.
Witam, jak w programie 3D Grapher wprowadzić wykres z=x^2+y^2 ?
jak wpisać arctangensa?
Normalnie: arctg(…).
WolframAlpha odpisze, że zrozumiał to jako t{{g}^{-1}}\left( \ldots \right)i to się ZGADZA, tak jest po “amerykańsku” arcus tangens.
Mam gorącą prośbę, mógłby mi ktoś obliczyc taką pochodną : x^3/(x-1)^2, chodzi mi o dziedzine, granice na koncach przedzialow, cechy szczegolne, miejsca przeciecia sie z osiami, monotonicznosc i ekstremum, druga pochodna tabelka i wykres. Mam takie zadanie a kompletnie go nie umiem;/
jak wpisać pierwiatek 5 stopnia?
x^(1/5)
Jak zapisać pierwiastek stopnia trzeciego?
x^(1/3)
W jaki sposób wprowadzić liczbę ‘pi’ do kalkulatora?
Po prostu trzeba było napisać ‘pi’, już rozgryzłem.