Kilka rzeczy, których powinieneś się dobrze nauczyć w średniej, ale nikt Ci tego nie powiedział – część 2 Kwantyfikatory

---

Kwantyfikatory – ale tego to w sumie nawet nie było….

No dobra, nie jestem na 100% pewien czy po regularnych, corocznych cięciach materiału kwantyfikatory w ogóle ostały się w szkole średniej. Nie bardzo też chce mi się nawet sprawdzać, bo po co się denerwować.

Powinny być jeszcze na rozszerzonym profilu. Naprawdę powinny.

No dobra, ale po co to komu?

W większości matematycznych definicji i twierdzeń używa się pojęć takich jak: “każdy” i “istnieje”.

Najczęściej w jakiś bardziej złożonych sekwencjach, na przykład “pomiędzy każdymi dwiema liczbami znajduje się nieskończenie wiele liczb” (to takie trochę półformalne i nieścisłe w sumie), albo: “dla każdej nieujemnej liczby rzeczywistej istnieje dokładnie jeden jej pierwiastek”, albo: “istnieje coś-tam-coś-tam, że dla każdego co-innego-coś-tam istnieje jeszcze-inne-coś-tam-coś-tam” (jest to matematyczna definicja jeszcze-innego-czegoś-tam).

Na studiach dostaniesz całą furę w taki sposób podanych definicji i twierdzeń, podyktowanych na szybko i ciurkiem na wykładzie, albo – co gorsza – napisanych od razu na tablicy w postaci:

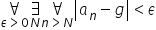
Dobrze więc by było (zamiast podnosić rękę i pytać się Pana Profesora, czy macie to “przerysować”), żebyś już na starcie umiał takie formuły prawidłowo przeczytać. Mógłbyś wtedy właściwie przejść już od razu do etapów “wgryzania się” w definicję, kilku obserwacji “jak działa” na konkretnych przykładach itd.

Kwantyfikator ogólny i szczegółowy – poznajmy się bliżej

“każdy”, “dla każdego” – to kwantyfikator ogólny, oznaczany jako:  .

“istnieje”, “istnieje takie” – to kwantyfikator szczegółowy, oznaczany jako: .

Stosuję i zalecam takie akurat znaczki zapisu kwantyfikatorów, bo się ze sobą na pewno nie pomylą.

 – to odwrócona litera wielkie A (od angielskiego “all” – każdy).

 – to odwrócona litera wielkie E (od angielskiego “exists” – istnieje).

Funkcjonują też inne oznaczenia na kwantyfikatory: Λ (“dla każdego”) i V (“istnieje”) – ale tymi się zajmować na będę, bo się każdemu mylą.

Formuły matematyczne zapisywane za pomocą kwantyfikatorów

Najprostsze formuły są postaci:

– czytamy: “dla każdego x” (można też zapisać: , ale znowu się myli, więc nie będę tego robić)

– czytamy: “istnieje x”

Na ogół jednak formuły są bardziej skomplikowane, na przykład:

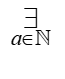– czytamy: “istnieje a będące liczbą naturalną”, albo: “istnieje takie a, należące do liczb naturalnych”, czy jakieklwiek inne wyrażenie w języku polskim, oddające istotę sprawy, mianowicie że:

1. Istnieje a

2. a jest liczbą naturalną

Nie ma tu jakiś “sztywnych” językowych reguł na temat jakie musi być każde słówko i czy musi być “istnieje a”, czy też musi być “istnieje takie a”.

Formuły można i najczęściej trzeba, łączyć ze sobą, na przykład:

\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,

znaczy:

“dla każdego x>4 istnieje takie n należące do liczb naturalnych”

Rozumiemy przez to, że dla każdego x>4 “znajdziemy” jakby n należący do liczb naturalnych, że do każdego takiego x “dobierzemy” odpowiednie n. Kwantyfikatory pozostają ze sobą w logicznym związku, to nie są dwie niezależne formuły zapisane koło siebie.

Co więcej…

Kolejność ma znaczenie

Taką samą formułę jak ostatnia, tylko z zamienioną kolejnością kwantyfikatorów:

\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,

…przeczytamy już inaczej:

“istnieje takie a będące liczbą naturalną, że dla x większych od 4…”

Rozumiemy, że chodzi o to, że najpierw mamy jakieś n (o którym wiemy, że istnieje) i tylko dla tego ustalonego n zachodzi coś takiego, że dla wszystkich x>4 coś tam się dzieje.

Przykład – dygresja

Klasycznym przykładem jest tutaj definicja jednostajnej i punktowej zbieżności ciąg funkcyjnego, które różnią się tylko… kolejnością kwantyfikatorów (trochę uprościłem te definicje):

Zbieżność punktowa:

Zbieżność jednostajna:

W definicji zbieżności jednostajnej kwantyfikator, który był na początku punktowej wylądował na końcu. Nie wchodząc w szczegóły zmienia to sens całej formuły.

W zbieżności punktowej NAJPIERW (czytamy od lewej) braliśmy jakiegoś dowolnego x, potem odczytując formułę dochodziliśmy do tego, że dla tego ustalonego na początku x odległości pomiędzy wartościami funkcji z ciągu i funkcji “granicznej” maleją w nieskończoność.

W zbieżności funkcji jednostajnej NAJPIERW stwierdzaliśmy, że odległość pomiędzy wartościami odpowiednich funkcji maleje w nieskończoność, a później dochodziliśmy do tego, że tak się dzieje dla dowolnego x-sa.

Zapis definicji, twierdzenia

Umiejąc czytać kwantyfikatory zapis matematycznych definicji i twierdzeń jest już dla nas otwarty. Na przykład:

\underset{x\in\mathbb{R}}{\mathop{\forall }}\,{{x}^{2}}\ge 0

Przeczytamy jako: “Dla każdej liczby rzeczywistej x , x do kwadratu jest większe lub równe zero”, albo jakoś ładniej: “Każda liczba x podniesiona do kwadratu jest nieujemna” – zdecydowanie jestem za odczytywaniem definicji i twierdzeń jakimś bardziej barwnym językiem.

Zdanie powyżej jest PRAWDZIWE. Nie ma żadnego problemu, żebyśmy pisali też sobie zdania FAŁSZYWE:

\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1

Czyli przeczytalibyśmy: “Istnieje taka liczba dodatnia a, że dla każdej liczby x większej od tej a, a podzielone przez ten x jest większe od 1”, co jest oczywiście FAŁSZEM (bo liczba dodatnia podzielona przez większą od niej nigdy nie będzie większa od 1 i nie ma takiej liczby).

A biorąc teraz na warsztat definicję granicy ciągu z poprzedniego postu:

Przeczytamy ją tak (dodając trochę objaśnień):

“Dla dowolnego większego do zera znajdziemy taki numer wyrazu ciągu , że dla każdego wyrazu ciągu o numerze większym od odległość (wartość bezwzględna to odległość) pomiędzy tym wyrazem ciągu a granicą będzie mniejsza od ”

Można też użyć jakoś bardziej ludzkiego języka:

“Jakbyśmy sobie nie ustawili małą odległość na początku, znajdziemy taki numer wyrazu ciągu, że wszystkie następne wyrazy tego ciągu będą bliżej granicy , niż ustalona na początku odległość “