Wzory na pochodne
Temat: Wzory na pochodne – wprowadzenie. Wyprowadzenie wzoru na pochodną z funkcji potęgowej.
Streszczenie
Na wykładzie pokażę, w jaki sposób wyprowadzać wzory na pochodne i sam wyprowadzę wzór na pochodną funkcji potęgowej 🙂
Wyprowadzanie wzorów na pochodna – ogólna metoda postępowania
Wzory na pochodne zawarte tablicach, podawanie na wykładach, ćwiczeniach nie wzięły się z kosmosu. Pochodna z funkcji f(x) w punkcie ![]() , jak wiemy z poprzednich wykładów to pewnego rodzaju granica funkcji, mianowicie:
, jak wiemy z poprzednich wykładów to pewnego rodzaju granica funkcji, mianowicie:
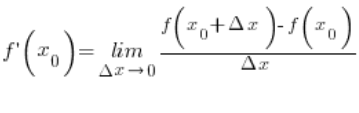
Aby wyprowadzić ogólny wzór na pochodną w dowolnym punkcie (bez ograniczania się do tylko do punktu ![]() ) wystarczy więc obliczyć ogólną granicę…
) wystarczy więc obliczyć ogólną granicę…
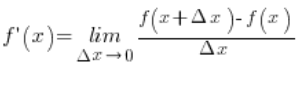
…której wynik oznaczać będzie wartość pochodnej w punkcie x. Rozwiązując powyższą granicę otrzymamy wzór na pochodną funkcji f(x).
Przykład 1 – wzór na pochodną funkcji potęgowej z wykładnikiem naturalnym
Chyba najczęściej używanym wzorkiem na pochodną, jest wzór na pochodną z funkcji potęgowej ![]() :
:
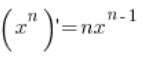
Wyprowadźmy go. Sprawdzimy, skąd się wziął 🙂
Na początku załóżmy, że liczba 'n’ jest liczbą naturalną. Dowolną. Nie ograniczamy się więc tylko do jednej funkcji. Nasze funkcje, których pochodną mamy wyprowadzić były by to na przykład: ![]() i każdą z nich „obejmujemy” jakby tym wzorem.
i każdą z nich „obejmujemy” jakby tym wzorem.
Pochodna z funkcji ![]() wyglądać będzie (z definicji pochodnej – bo jaki wynik mamy dostać na końcu to już wiemy z tablic) tak:
wyglądać będzie (z definicji pochodnej – bo jaki wynik mamy dostać na końcu to już wiemy z tablic) tak:
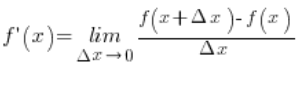
Teraz zastanówmy się chwilkę. ![]() – ten wzór oznacza, że każdemu argumentowi funkcji przyporządkowujemy wartość równą temu argumentowi podniesionemu do n-tej potęgi. Ile więc równa będzie
– ten wzór oznacza, że każdemu argumentowi funkcji przyporządkowujemy wartość równą temu argumentowi podniesionemu do n-tej potęgi. Ile więc równa będzie ![]() . Konsekwentnie – funkcja f przyporządkowuje każdemu argumentowi ten argument podniesiony do n-tej potęgi, otrzymamy więc:
. Konsekwentnie – funkcja f przyporządkowuje każdemu argumentowi ten argument podniesiony do n-tej potęgi, otrzymamy więc: ![]() .
.
Wracając do naszej granicy:
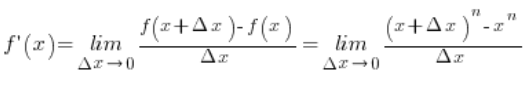
Teraz zatrzymajmy się już na naprawdę dłuższą chwilę, żeby zastanowić się, jak rozpisać wyrażenie: ![]() . Oczywiście absolutnie nie:
. Oczywiście absolutnie nie: ![]() . Nie, nie, nie. Nie.
. Nie, nie, nie. Nie.
Skorzystamy tutaj z tzw. wzoru Newtona (może miałeś w szkole średniej, a może nie miałeś):
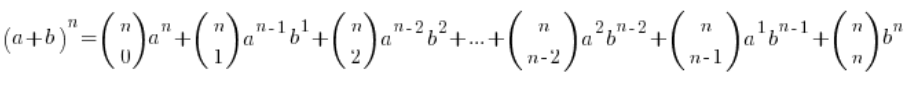
Gdzie te dziwne znaczki w nawiasach (nie mylić z ułamkami w nawiasach) to tzw. symbole Newtona, liczone wg. wzoru:
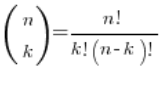
Na przykład:
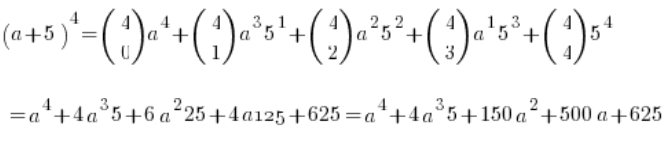
Wzór Newtona można udowodnić indukcyjnie, zatem dotyczy on tylko n naturalnych (można go uogólnić, ale zostawmy to). Niestety, żeby nie rozwlekać wykładu nie będę tego robił. Jeśli kompletnie się w tym momencie zgubiłeś, może rozważ zrobienie krótkiej przerwy i porobienie kilku ćwiczeń z zakresu wzoru Newtona -wystarczy (oczywiście jeśli będzie Ci się chciało go udowadniać to w ogóle super) 🙂
Przypomnijmy teraz naszą pochodną-granicę do policzenia:
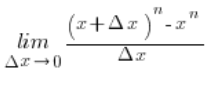
Korzystając w liczniku ze wzoru Newtona otrzymamy:

Wyłączając wspólny czynnik ![]() przed nawias w liczniku mam:
przed nawias w liczniku mam:
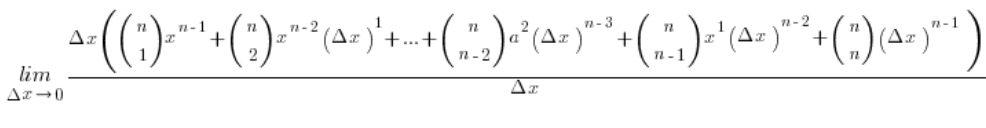
![]() się skraca i mam:
się skraca i mam:
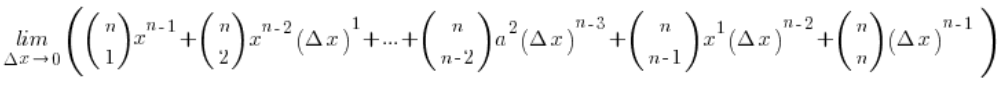
Jeśli ![]() składniki z
składniki z ![]() się skrócą i wyjdę na:
się skrócą i wyjdę na:
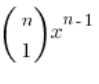
Teraz:
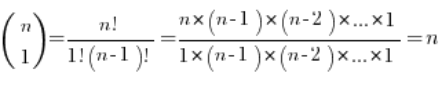
Czyli nasza granica równa jest:
![]()
Co też było dokładnie do wykazania.
W naszym przykładzie 1 założyliśmy jednak, że n jest liczbą naturalną. Mamy więc wzór na pochodną z funkcji ![]() itd. ale nie mamy wykazanego wzoru na pochodną z funkcji np.
itd. ale nie mamy wykazanego wzoru na pochodną z funkcji np. ![]() albo
albo ![]() .
.
Przykład 2 – wzór na pochodną funkcji potęgowej z wykładnikiem rzeczywistym
Wykażemy teraz wzór: 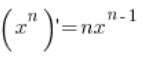 nie ograniczając się tylko do n będących liczbami naturalnymi. Nasz wzór obejmie więc też przypadki pochodnych z funkcji
nie ograniczając się tylko do n będących liczbami naturalnymi. Nasz wzór obejmie więc też przypadki pochodnych z funkcji ![]() ,
,![]() itd.
itd.
Wychodząc ze wzoru na pochodną jako granicę funkcji dostaniemy:
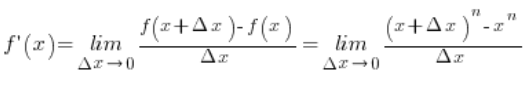
Wzór Newtona z przykładu 1 tym razem nie będzie nam pomocą (przynajmniej w takiej postaci, w jakiej go tam wprowadziliśmy).
Aby obliczyć powyższą granicę, a więc wyprowadzić wzór na pochodną doprowadzimy ją do wzoru:
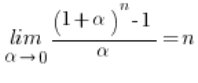
Najpierw jednak udowodnijmy ten wzór.
Mamy do policzenia:
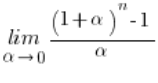
Stosujemy podstawienie:
![]()
Z którego wynika, że:
![]()
A po zlogarytmowaniu obu stron:
![]()
A to ze znanego wzoru na logarytmy równe jest:
![]()
Czyli:
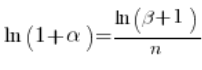
Wracamy teraz do naszej granicy i przekształcamy ją (korzystając z powyższych zależności):
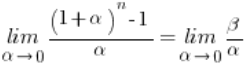
Ta granica równa jest:
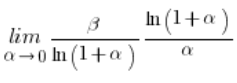
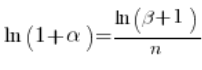 (wyprowadziliśmy to wyżej) zatem mamy:
(wyprowadziliśmy to wyżej) zatem mamy:
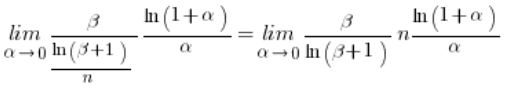
Zarówno 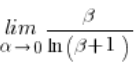 jak i
jak i 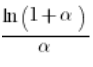 dążą do 1 (z podstawowego wzoru na granice funkcji), zatem pokazaliśmy, że:
dążą do 1 (z podstawowego wzoru na granice funkcji), zatem pokazaliśmy, że:
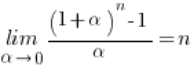
Wracajmy więc do naszej granicy funkcji:
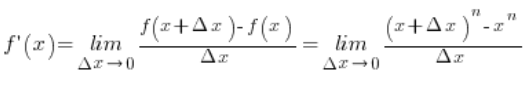
Przekształcamy, wyciągając w nawiasie x przed nawias:
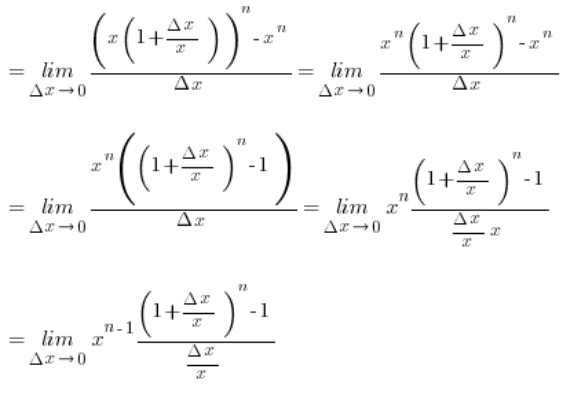
Tu korzystamy z udowodnionego wyżej wzoru:
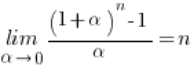
I mamy:
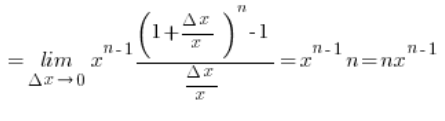
Zatem wzór został udowodniony dla dowolnych n, nie tylko naturalnych!
Zastosowanie wzoru na pochodne funkcji potęgowej
Mając wyprowadzony wzór na pochodną funkcji potęgowej: 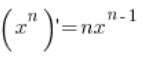 mamy do dyspozycji naprawdę potężne narzędzie do obliczania pochodnych nie tylko z prostych:
mamy do dyspozycji naprawdę potężne narzędzie do obliczania pochodnych nie tylko z prostych:
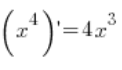
Ale i bardziej zakręconych funkcji:
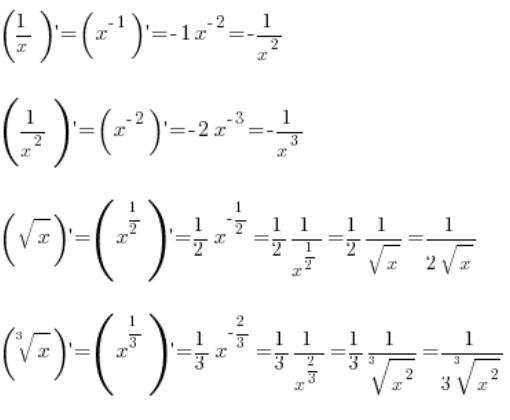
Podsumowanie
Jak widać na powyższym przykładzie, zagadnienie znalezienia ogólnego wzoru na pochodną funkcji f(x) sprowadza się do policzenia odpowiedniej granicy funkcji. Nie granicy z funkcji f(x), tylko granicy:
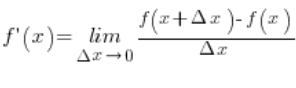
Szkolne przykłady na wykazywanie z definicji to wyprowadzanie wzorów na pochodne z funkcji liniowej, kwadratowej, pierwiastka, sinusa lub cosinusa. Zachęcam Cię jednak to próby swoich sił z wyprowadzaniem jakiś innych ciekawych wzorów na pochodne, na przykład na pochodną z funkcji e do x, albo z jakiejś funkcji wykładniczej, albo z tangensa…
Powodzenia!
KONIEC
Pisząc tego posta korzystałem z…
1. „Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.

Michau
Genialne i genialny cały blog.
Sporo się naszukałem zanim trafiłem na tę stronkę. Wyszukiwarka z maniakalnym uporem kierowała mnie do stron z informacjami czym jest pochodna i przykładami jak ją policzyć, natomiast żadna z nich nie dawała odpowiedzi jak wyznaczyć wzór na pochodną.
Gorąco polecam !!!
Piter
Świetne, dzięki ! 🙂