Pochodne funkcji jako tangensy

Pochodne Funkcji Wykład 2

Temat: Pochodne funkcji jako tangensy nachylenia stycznej

Streszczenie

Na poprzednim wykładzie wprowadziliśmy pojęcie pochodnej funkcji jako pewnego rodzaju “prędkości” (rozumiejąc te słowo szerzej, niż tylko jako prędkość fizyczną). Na tym wykładzie będziemy wprowadzać dokładnie to samo – czyli pochodną funkcji – ale od innej strony, bardziej geometrycznej, poprzez pojęcie stycznej.

Co to jest styczna?

Ze styczną jak z koniem – jaka jest, każdy widzi. Każde dziecko rozumie, że styczna do wykresu w punkcie A wygląda jakoś mniej więcej tak…

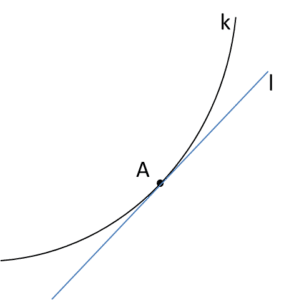…problem jest z tym, jak to właściwie opisać słowami i zdefiniować. Maślana definicja: “styczna to prosta, która się styka” nie wystarczy. Maślane definicje to takie, które zawierają błąd logiczny polegający na odwołaniu się w definicji do pojęcia, które właśnie mamy zdefiniować. Nie można zdefiniować masła jako “coś, co jest maślane” – bo nie wiemy, co jest “maślane”, nie mając definicji masła. Tak samo nie możemy użyć w definicji stycznej słowa “styka”, bo nie wiemy jeszcze, nie zdefiniowaliśmy tego, co znaczy właściwie “styka”.

Może więc tak:

Definicja (zła)

Styczna do krzywej w punkcie A to prosta, która ma z nią tylko jeden punkt wspólny i jest to punkt A.

Taka definicja wygląda już na pewno lepiej. Pasuje do poznanych w szkole średniej stycznych do okręgu. Ale zgodnie z nią, coś takiego…

… również przedstawia styczną do krzywej k (bo ma z krzywą k tylko jeden punkt wspólny A), a także widać, że…

…tych niby “stycznych” do krzywej było by nieskończenie wiele! Czy jednak o to nam chodziło? Stanowczo nie. Styczna miała być jedna i miała wyglądać, przypominam, tak:

Jej ścisła definicja (bo nieformalnie wszyscy, jak mówiłem, wiemy, o co chodzi) jest bardziej skomplikowana, niż by się mogło wydawać.

Zacznijmy od pojęcia cięciwy. Odchodzimy od znanej nam z podstawówki cięciwy okręgu, uogólniamy pojęcie i mamy…

Definicja cięciwy

Cięciwą nazywamy odcinek łączący dwa dowolne punkty krzywej.

Narysujmy kilka cięciw, mających mających początek/koniec w punkcie A:

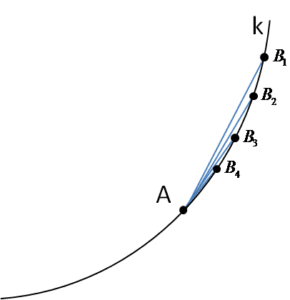Każda cięciwa wyznacza sieczną:

Definicja siecznej

Sieczna to prosta, w której zawiera się cięciwa (inaczej: prosta przecinająca krzywą w co najmniej dwóch punktach).

Narysujmy więc nasze sieczne, przechodzące przez punkt A:

Zauważmy teraz ważną rzecz – przybliżając się z punktami do punktu A odpowiednie sieczne sieczne coraz bardziej i bardziej przypominają naszą styczną l (zaznaczoną na czerwono):

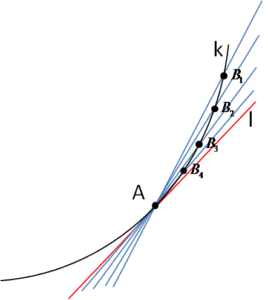
Tak właśnie należy zdefiniować styczną do krzywej w punkcie A. Jak prostą graniczną dla siecznych , gdzie punkty  przybliżają się coraz bardziej do punktu A.

Tangens nachylenia stycznej (współczynnik kątowy)

Narysujmy którąś, przykładową sieczną, tym razem już w układzie współrzędnych:

Rozpatrzmy “nachylenie” tej siecznej, czyli jakby miarę tego, jak “stromo” ta sieczna rośnie. Za taką miarę przyjmijmy współczynnik kierunkowy prostej, przez który będziemy rozumieć tangens kąta  , jak na rysunku:

Kąt jest to kąt pomiędzy prostą równoległą do osi OX i przechodzącą przez punkt A, a naszą sieczną. Będziemy mówić i rozumieć w skrócie, że jest to kąt pomiędzy osią OX, a sieczną (oczywiście jest on taki sam).

Tangens kąta jak na rysunku nadaje się świetnie do oznaczenia tego, jak “stroma” jest prosta. Im większy przyrost wartości funkcji   dla przyrostu argumentów – tym większy będzie kąt , a w konsekwencji tym większy jego tangens, który (przypominamy ze średniej) jest dzieleniem przyprostokątnej leżącej naprzeciwko kąta do przyprostokątnej przyległej do kąta, czyli:

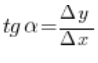
Teraz wyobraźmy sobie, że rysujemy kolejne sieczne, biorąc punkty coraz bliżej punktu A. Dla każdej z takich siecznych uzyskamy inny 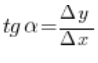, a będą one coraz bliższe dokładnemu współczynnikowi kierunkowemu stycznej. Można powiedzieć, że współczynnik kierunkowy stycznej równy będzie granicy takiego ciągu współczynników kierunkowych siecznych, przy której (bo odległości punktów A od punktów są coraz mniejsze i mniejsze):

Tangens nachylenia stycznej=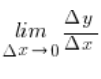

I jeśli tylko uświadomimy sobie, że – czyli że przyrost wartości funkcji równy jest wartości funkcji w punkcie A powiększonym o odjąć wartość funkcji w punkcie dokładnie A, dochodzimy do tego, że wartość tego tangensa (nachylenia stycznej) równa jest dokładnie wartości pochodnej funkcji w punkcie A z poprzedniego wykładu:

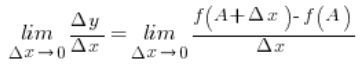
I że właściwie, jeśli umówimy się na definicję…

Definicja pochodnej funkcji w punkcie

Pochodną funkcji w punkcie nazywamy tangens nachylenia stycznej do jej wykresu w tym punkcie do osi OX.

Nie potrzebujemy do niczego poprzedniego wykładu, możemy zdefiniować sobie i rozumieć pochodne funkcji w taki sposób, nie mieszając do sprawy jakiegoś pojęcia “prędkości”. Takie podejście do pochodnych (nie poprzez granicę z prędkości średnich) możemy nazwać “interpretacją geometryczną pochodnej”.

Pochodne w punkcie jako tangensy nachylenia krzywych (przykłady)

Narysujmy kilka stycznych do krzywej w różnych punktach w układzie współrzędnych i zastanówmy się, jak ich tangens kąta nachylenia tych stycznych do wykresu będzie wpływał na wartość pochodnej w tych punktach.

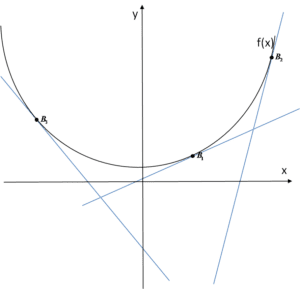Zauważmy, że styczna przechodząca przez punkt jest prostą malejącą. Styczne przechodzące przez punkty są prostymi rosnącymi. Różnią się jednak od siebie “nachyleniem” – prosta przechodząca przez punkt rośnie jakby “łagodnie”, a ta przechodząca przez jest bardziej “stroma”. (zauważmy, że dosyć dobrze odpowiada to zachowaniu się samego wykresu krzywej – tak, jak go omawialiśmy na poprzednim wykładzie).

Zaznaczmy teraz kąty nachylenia, odpowiednio :

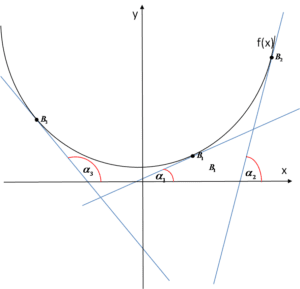Kąt jest mniejszy od kąta , jego tangens jest także mniejszy, zatem wartość pochodnej w punkcie jest mniejsza od wartości pochodnej w punkcie .

Co do kąta , jest on oczywiście większy od kątów , ale należy do przedziału , a w tym przedziale wartości tangensów są ujemne (można to sprawdzić na przykład na wykresie funkcji tangens x). Zatem wartości pochodnej funkcji będą ujemne również, co znajduje swoje odzwierciedlenie w wykresie stycznej – jest ona prostą malejącą. Przyrostowi argumentów odpowiada spadek (“przyrost ujemny” – nie znoszę tego wyrażenia) wartości .

KONIEC

Pisząc tego posta korzystałem z…

1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.

Kliknij, aby przypomnieć sobie, czym jest pochodna rozumiana jako prędkość (poprzedni Wykład) <–

Kliknij, aby zobaczyć, jak interpretacja geometrycznej pochodnej sprawdza się w szczególnych przypadkach – pochodnych jednostronnych i nieskończonych (następny Wykład) –>

Kliknij, aby wrócić na stronę z wykładami o pochodnych