Kalkulator Do Szeregów

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Przedstawiam kolejny kalkulator Wolphrama, przerobiony lekko przeze mnie.

Ta zabawka poniżej służy do obliczania sumy szeregów (nie tylko liczbowych, ale i funkcyjnych!):

Działa prosto, w polu “Szereg” wpisujemy wyraz ogólny szeregu, w polu “Od” początek indeksu (to, co jest na dole w znaku sigmy szeregu), w polu “Do” koniec indeksu. Domyślnie liczymy szeregi nieskończone, więc zostawiamy infinty, ale kalkulatorem policzymy też szereg skończony, wtedy wpisalibyśmy tam np. 100.

Oczywiście kalkulator dobrze posłuży nam także do typowych zadań typu “sprawdź, czy szereg jest zbieżny”. Po prostu liczymy sumę szeregu kalkulatorem i jeśli wyjdzie nam skończona liczba, to znaczy, że szereg jest zbieżny. Jeżeli szereg jest rozbieżny, kalkulator sam nam to oznajmi poprzez komunikat “does not converge” (nie zbiega).

Przykład

Zbadajmy sumę szeregu:

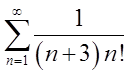
Wpisujemy odpowiednie wartości do kalkulatora:

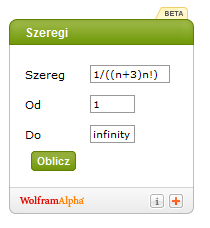, klikamy na ‘Oblicz’ i mamy wynik:

Sumą szeregu jest liczba: 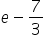$e minus 7 over 3$ , w przybliżeniu 0,384948. Oczywiście wynika z tego to, że jest on zbieżny. Jako bonus na dole mamy kilka reprezentacji tej liczby innym szeregami.

Jestem pewien, że ten kalkulator będzie super pomocą dla wszystkich liczących szeregi (można łatwo sprawdzić wynik).

Jak zawsze zapraszam do pytań i komentarzy pod postem!

Bestsellery

Kurs Macierze

Studia / Autor: mgr Krystian Karczyński

49,00 zł

Kurs Granice

Studia / Autor: mgr Krystian Karczyński

49,00 zł

Kurs Pochodne i Badanie Przebiegu Zmienności Funkcji

Studia / Autor: mgr Krystian Karczyński

49,00 zł

Kurs Mechanika - Kinematyka

Studia / Autor: mgr inż. Adam Kasprzak

49,00 zł

Zobacz wszystkie Kursy eTrapez

Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?

Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.

Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.

Dodaj komentarz Anuluj pisanie odpowiedzi

Sylwia pisze:

13 stycznia 2018 o 12:23

Witam chciałam obliczyć zbieżność szeregu, lecz nie bardzo umiem zinterpretować wynik ..Input \interpretation:Result:Convergence tests:z góry dziękuje za pomoc 🙂

Odpowiedz
Bartek pisze:

18 stycznia 2013 o 21:59

Witam, mam problem z szeregiem:

$sin((n+1/n)pi)$ przy n dążącym do nieskończoności od jedynki,
doprowadziłem go do postaci:
$((-1)^n)sin(pi/n)$
zbadałem bezwzględną zbieżność (nie jest), lecz jak sprawdzić warunkową zbieżność?

Odpowiedz
1. Ryhor Abramovich pisze:
  
  20 października 2016 o 11:16
  
  $sum from n equals 1 to infinity of sin open parentheses open parentheses n plus 1 over n close parentheses times \pi close parentheses$
  
  Rozwiązanie:
  
  Najpierw przekształczymy ten wyraz wg wzoru:
  
  $sin open parentheses x plus y close parentheses equals sin x times cos y plus cos x times sin y$ i otrzymamy:
  
  $sin open parentheses open parentheses n plus 1 over n close parentheses times straight \pi close parentheses equals sin open parentheses πn plus straight \pi over straight n close parentheses equals$ $sinπ n times cos straight \pi over n plus cosπ n times sin straight \pi over n$
  
  O ile $sinπ n equals 0 comma space cosπ n equals open parentheses negative 1 close parentheses to the power of n$ , to
  
  $sinπ n times cos straight \pi over n plus cosπ n times sin straight \pi over n equals 0 times cos straight \pi over n plus open parentheses negative 1 close parentheses to the power of n times sin straight \pi over n equals open parentheses negative 1 close parentheses to the power of n times sin straight \pi over n$ ,
  
  i wtedy
  
  $sum from n equals 1 to infinity of sin open parentheses open parentheses n plus 1 over n close parentheses times straight \pi close parentheses equals sum from n equals 1 to infinity of open parentheses negative 1 close parentheses to the power of n times sin straight \pi over n$
  
  Zbadamy najpierw zbieżność bezwzględną. Rozpatrzymy szereg
  
  $sum from n equals 1 to infinity of open vertical bar open parentheses negative 1 close parentheses to the power of n times sin straight \pi over n close vertical bar equals sum from n equals 1 to infinity of sin straight \pi over n$
  
  Ten szereg jest rozbieżny, np, pod względem kriterium porownawczego, o ile
  
  $sin \alpha almost equal to \alpha space$ przy $alpha \rightwards arrow 0$ , i możemy przyjąć, że
  
  $alpha equals straight \pi over n \rightwards arrow 0 space p r z y space n \rightwards arrow infinity$
  
  Wtedy szereg $sum from n equals 1 to infinity of sin straight \pi over n$ jest zbieżny lub rozbieżny razem z szeregiem
  
  $sum from n equals 1 to infinity of straight \pi over n equals straight \pi sum from straight n equals 1 to infinity of 1 over straight n$ ,
  
  a ten ostatni jest szeregiem rozbieżnym (szereg Dirichlet’a). Czyli szereg
  
  $sum from n equals 1 to infinity of open parentheses negative 1 close parentheses to the power of n times sin straight \pi over n$
  
  nie jest zbieżny bezwzględne.
  
  Sprawdzimy zatem zbieżność warunkową. Badamy kryterium Leibnitz’a, który mówi, ze szereg naprzemienny typu $sum from n equals 1 to infinity of open parentheses negative 1 close parentheses to the power of n times a subscript n$ jest zbieżny, gdy
  
  a) $limit as n \rightwards arrow infinity of a subscript n equals 0$ , i
  
  b) $a subscript n greater than a subscript n plus 1 end subscript$
  
  Liczymy:
  
  a) $limit as n \rightwards arrow infinity of sin straight \pi over n equals 0$ – zachodzi,
  
  b) $a subscript n equals sin straight \pi over n greater than sin fraction numerator straight \pi over denominator n plus 1 end fraction equals a subscript n plus 1 end subscript$ – też żachodzi, ponieważ $straight \pi over n greater than fraction numerator straight \pi over denominator n plus 1 end fraction$ , a funkcja
  
  $y equals sin x$ jest malejąca w I czwiartku ( $straight \pi over n \rightwards arrow 0 space p r z y space n \rightwards arrow infinity$ )
  
  W związku z tym szereg
  
  $sum from n equals 1 to infinity of sin open parentheses open parentheses n plus 1 over n close parentheses times straight \pi close parentheses equals sum from n equals 1 to infinity of open parentheses negative 1 close parentheses to the power of n times sin straight \pi over n$
  
  jest zbieżny warunkowo.
Matibob pisze:

8 lutego 2012 o 20:25

Dzięki kolego, spać przez to nie mogłem.

Odpowiedz
Matibob pisze:

8 lutego 2012 o 10:40

Przesuń stronę bardziej w prawo, tam jest schowany znak X.

Odpowiedz
Matibob pisze:

7 lutego 2012 o 15:09

Jak zlikwidować tą zieloną ramkę góry po prawej?

Odpowiedz