Streszczenie
W artykule przedstawiam metodę Gaussa-Jordana na obliczanie macierzy odwrotnych, która sprawdza się dobrze dla macierzy o wymiarach większych niż ![]() .
.
Macierze odwrotne różnych wymiarów – dobór metody
Macierze odwrotne można liczyć ze wzoru:
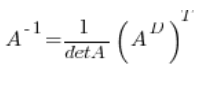
Sprawdza się to dobrze w macierzach rzędu ![]() i
i ![]() . W przypadku wymiaru
. W przypadku wymiaru ![]() :
:
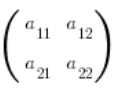
…do macierzy dopełnień ![]() potrzebujemy cztery dopełnienia algebraiczne (będą to wyznaczniki macierzy stopnia 1). Bułka z masłem. Do macierzy odwrotnej wymiaru
potrzebujemy cztery dopełnienia algebraiczne (będą to wyznaczniki macierzy stopnia 1). Bułka z masłem. Do macierzy odwrotnej wymiaru ![]() :
:
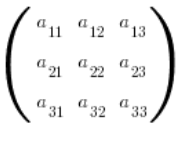
…musimy policzyć już dziewięć dopełnień algebraicznych (wyznaczniki stopnia 2). Jak najbardziej do zrobienia.
Wyobraźmy sobie jednak macierz wymiaru ![]() :
:
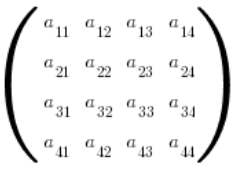
Jej wyznacznik stopnia czwartego jest jeszcze do przejścia. Ale wyobraź sobie macierz dopełnień… Przed nami 16 (słownie: szesnaście) wyznaczników trzeciego stopnia! Zadanie na długie zimowe wieczory, a pamiętajmy, że jeden drobny błąd w gąszczu obliczeń rozkłada całe zadanie.
Obliczanie macierzy wymiarów większych niż ![]() metodą macierzy dopełnień pozostawiam już bez komentarza.
metodą macierzy dopełnień pozostawiam już bez komentarza.
Wyjście?
Macierze odwrotne metoda Gaussa-Jordana
Metoda Gaussa-Jordana jest metodą dosyć żmudną, ale bez porównania mniej żmudną niż próba obliczania z wykorzystaniem dopełnień algebraicznych macierzy odwrotnych wymiaru ![]() i większych. Opiera się ona na zastosowaniu sztuczek wykorzystywanych już w metodzie Gaussa rozwiązywania układów równań liniowych na wierszach – ale musimy ich stosować więcej.
i większych. Opiera się ona na zastosowaniu sztuczek wykorzystywanych już w metodzie Gaussa rozwiązywania układów równań liniowych na wierszach – ale musimy ich stosować więcej.
Uwaga!
W metodzie Gaussa-Jordana możemy wykorzystywać tylko operacje elementarne na wierszach. Nie można zamieniać kolumn miejscami. Ograniczenie to powoduje, że w wielu przykładach będzie nam się robić o wiele ciężej, a często zabrnięcie w ułamki będzie nieuniknione.
Zamiast macierzy trójkątnej będziemy chcieli uzyskać macierz jednostkową, co będzie wymagało wykonania znacznie większej ilości operacji (i tylko na wierszach). Oczywiście zanim nauczymy się tej metody silnie zalecam naprawdę solidne przerobienie metody Gaussa rozwiązywania układów równań liniowych.
Jak to się robi?
Startujemy mając do policzenia macierz odwrotną do jakiejś ![]() .
.
Budujemy wielgachną (na ogół) macierz:
![]()
…gdzie po lewej stronie kreski jest nasza macierz, do której odwrotną mamy policzyć, a po prawej stronie kreski macierz jednostkowa (kwadratowa, która na głównej przekątnej ma jedynki a poza nimi same zera). Potem, korzystając z operacji elementarnych znanych z metody Gaussa rozwiązywania układów równań liniowych (np. dodawanie do siebie wierszy po przemnożeniu ich przez jakąś liczbę), przekształcamy tą wielgachną macierz do postaci:
![]()
… w której macierz B po prawej stronie kreski to jest już nasz wynik, czyli macierz odwrotna ![]() .
.
Łatwo powiedzieć, trudniej zrobić? Ano zobaczmy na konkretnym przykładzie.
Przykład
Weźmy macierz ![]() :
:
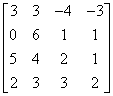
Zadanie polega na obliczeniu do niej macierzy odwrotnej. Zrobimy to metodą Gaussa-Jordana. Tworzymy odpowiednią macierz:
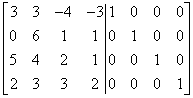
Po lewej stronie kreski mamy macierz, do której odwrotną trzeba policzyć, a po prawej macierz jednostkową (odpowiedniego wymiaru oczywiście). Nasze zadanie polega na tym, żeby sytuację odwrócić, tzn. po lewej stronie kreski mieć macierz jednostkową, a po prawej inną (która będzie naszym wynikiem – tak przy okazji).
Pracuję tak, jak to się robiło w rozwiązywaniu układów równań liniowych metodą Gaussa, ale z naciskiem, żeby na przekątnej mieć jedynki, oraz nie zamieniając kolumn miejscami (bo mogę pracować tylko na wierszach) . Zaczynam więc od pierwszej kolumny i manipuluję tak, aby w odpowiednim miejscu (czyli w pierwszym wierszu i pierwszej kolumnie) otrzymać jedynkę.
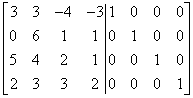
Pomnożenie pierwszego wiersza przez ![]() wtrąci nas w ułamki. Tego nie chcemy i będziemy się przed tym bronić do końca. Żeby uzyskać jedynkę w pierwszym wierszu i pierwszej kolumnie mnożę czwarty wiersz przez -1 i dodaję do pierwszego, uzyskując:
wtrąci nas w ułamki. Tego nie chcemy i będziemy się przed tym bronić do końca. Żeby uzyskać jedynkę w pierwszym wierszu i pierwszej kolumnie mnożę czwarty wiersz przez -1 i dodaję do pierwszego, uzyskując:
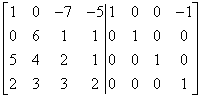
Teraz zeruję pierwszą kolumnę, mnożąc pierwszy wiersz przez -5 i dodając do trzeciego:
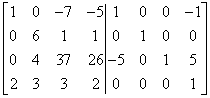
…oraz mnożąc pierwszy wiersz przez -2 i dodając do czwartego:
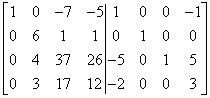
Pierwsza kolumna jest już „cacy” – taka, jaka powinna być w macierzy jednostkowej. Idziemy do drugiej. Najpierw musimy skombinować jedynkę w drugim wierszu drugiej kolumny (tam, gdzie jest w macierzy jednostkowej). W tej chwili jest tam 6. Pomnożenie przez ![]() również wciągnie nas w ułamki. Tego nie chcemy. Zamiast tego mnożę czwarty wiersz przez -1 i dodaję do trzeciego:
również wciągnie nas w ułamki. Tego nie chcemy. Zamiast tego mnożę czwarty wiersz przez -1 i dodaję do trzeciego:
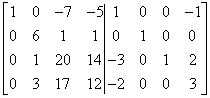
…i mam jedynkę w trzecim wierszu macierzy (czyli jeszcze nie tam, gdzie trzeba). Teraz zamieniam trzeci i drugi wiersz miejscami:
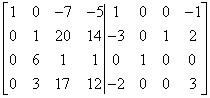
Mam jedynkę we właściwym miejscu. Teraz zeruję drugą kolumnę (wiersz pierwszy zostawiam w spokoju, bo tam jest już zero). Mnożę drugi wiersz macierzy przez -6 i dodaję do trzeciego:
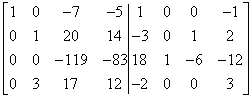
Mnożę drugi wiersz macierzy przez -3 i dodaję do czwartego:
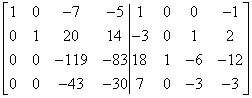
Mamy wyzerowaną drugą kolumnę macierzy. Przechodzimy do trzeciej.
Tutaj czeka nas prawdziwe wyzwanie. Jedynkę musimy zrobić w miejscu -119. Manipulować mogę już tylko trzecim i czwartym wierszem macierzy, bo gdybym ruszył pierwszy albo drugi zepsułbym już ustawione kolumny.
Mnożę czwarty wiersz przez -3 i dodaję do trzeciego:
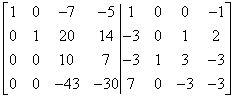
Walczę o jedynkę bez wchodzenia ułamki dalej, nie dzielę więc trzeciego wiersza przez 10. Zamiast tego mnożę trzeci wiersz przez cztery i dodaję do czwartego:
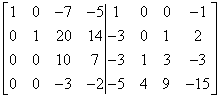
…a potem mnożę czwarty przez 3 i dodaję do trzeciego:
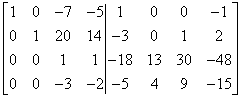
Mam jedynkę i udało się uniknąć ułamków idzie mi więc naprawdę nieźle. Teraz zeruję CAŁĄ trzecią kolumnę (a więc elementy pierwszego, drugiego i czwartego wiersza) poprzez:
– pomnożenie trzeciego wiersza przez 7 i dodanie do pierwszego
– pomnożenie trzeciego wiersza przez -20 i dodanie do drugiego
– pomnożenie trzeciego wiersza przez 3 i dodanie do czwartego
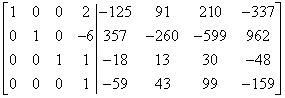
Trzecia kolumna przygotowana. Przechodzę do czwartej.
Bardzo fartownie w odpowiednim miejscu macierzy (czwarty wiersz i czwarta kolumna) mamy już jedynkę. Jeśli tam nie było by jedynki pozostało nam by już tylko jedno wyjście: podzielić czwarty wiersz przez odpowiednią liczbę, nawet jeśli oznaczało by to powstanie ułamków. Ale szczęśliwie możemy z miejsca zerować czwartą kolumnę, poprzez:
– pomnożenie czwartego wiersza przez -2 i dodanie do pierwszego
– pomnożenie czwartego wiersza przez 6 i dodanie do drugiego
– pomnożenie czwartego wiersza przez -1 i dodanie do trzeciego
W ten sposób dotarliśmy do celu! Po lewej stronie kreski mamy macierz jednostkową, a po prawej macierz odwrotną, którą szukamy.
Teraz już tylko zapisać odpowiedź:
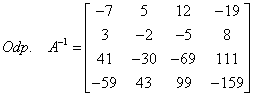
Nie wierzysz, że odpowiedź jest prawidłowa? Sprawdź mnie, mnożąc macierz, do której odwrotną mieliśmy policzyć:
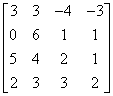
przez macierz wynikową:
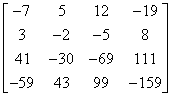
wynikiem powinna być macierz jednostkowa! 🙂

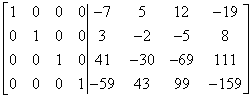
super, potrzebne na bardziej wymagających matematycznie studiach
Boniek
Czy metoda gaussa, jest równoważna metodzie macierzy rozszerzonej. Na mojej uczelni pani profesor wymaga zastosowanie metody macierzy rozszerzonej do wyliczania macierzy odwrotnej, czy stosujac metode gaussa również wynik zostanie uznany?
kkk
a jeśli z 0( które stoi na przekątnej) chce zrobić tą jedynkę to co musze wykonać?
Krystian Karczyński
Zamienić któreś wiersze miejscami.
Bartek
Kurde Mistrzu wymiatasz gdyby nie Ty cala moja matma na studiach to bylaby jedna wielka niekonczaca sie poprawka. Pozdrawiam, oby tak dalej !
Bart
Szczególnie jak się wybrało informatykę po klasie biologiczno-chemicznej. 😀
Marcin
Czy przy odwracaniu macierzy mogę sobie upraszczać wiersze? Np. jeśli wszystkie elementy w wierszu dzielą się przez 2 to czy mogę je wszystkie podzielić?
Stanisław wojcik
Mozna ale na końcu nalezy pomnożyć przez ten podzielenia dowolny wiersz macierzy odwrotnej
Stanisław wojcik
Pisałem , ze mozna z zastrzeżeniem .Mozna bez zadnych ograniczeń nie tylko dzielic ale rowniez mnożyć wiersze przez te sama liczbę .Przykladowo jeśli w element wiersza stanowi liczba różna od jedności a potrzebna zamiast tej liczby jedynka nalezy podzielic prze te liczbę wszystkie elementy wiersza .Mozna takze mnożyć , aby pozbyc sie ulamkow .Proponuje stosowanie mojej metody.Przez wydzielanie tworzyć potrzebne jedynki na przekątnej macierzy danej w kolejności od pierwszej kolumny .Majac jedynkę łatwiej wtedy uzyskiwać zera poza przekątna macierzy dla ktorej mamy obliczyć macierz odwrotna .Te działania powtórzyć w kolejnych kolumnach .Metodą uniwersalna , ktora realizuje komputer (głupi) a student jest wiele wiele mądrzejszy od komputera .
Magda
I jest też mały błąd w macierzy jednostkowej bo zamiast zer w czwartej kolumnie jest -6 i 1. Ale ogólnie wiadomo o co chodzi, super wytłumaczone 😉 dzięki Krystian!
Krystian Karczyński
Zgadza się, dzięki!
Kamil
„Mamy wyzerowaną drugą kolumnę macierzy. Przechodzimy do trzeciej.
Tutaj czeka nas prawdziwe wyzwanie. Jedynkę musimy zrobić w miejscu -119. Manipulować moge już tylko trzecim i czwartym wierszem macierzy, bo gdybym ruszył pierwszy albo drugi zepsułbym już ustawione kolumny.
Mnożę trzeci wiersz przez 4 i dodaję do czwartego:”
Tu chyba jest błąd. Patrząc na macierz pod tym tekstem zauwazyłem, że tak na prawde przemnożył Pan 4 wiersz przez -3 i dodał do trzeciego 🙂
Krystian Karczyński
Tak, dokładnie, ma Pan rację, w opisie jest błąd. Powinno być: „Mnożę czwarty wiersz przez -3 i dodaję do trzeciego:…”. Przepraszam i dziękuję za zwrócenie uwagi.