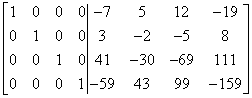Summary
In the article I present the Gauss-Jordan elimination method for calculating inverse matrix, which works well for matrix with dimensions larger than![]() .
.
Inverse matrix of various dimensions – selection of method
Inverse matrix can be calculated from the formula:
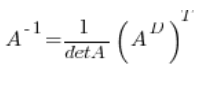
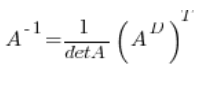
This works well for row matrices![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
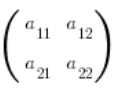

…to the adjugate matrix![]()
![]()
To the inverse dimension matrix![]()
![]()
![]()
![]()
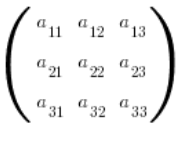

…we have to count nine algebraic adjugates (determinants of degree 2). Absolutely doable.
But let’s imagine a matrix![]()
![]()
![]()
![]()
![]()
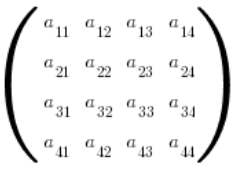

Its fourth degree determinant is still to be passed. But imagine an adjugate matrix… There are 16 (in words: sixteen) third-degree determinants ahead of us! A task for long winter evenings, and remember that one small error in the thicket of calculations destroys the entire task.
Calculating a matrix of dimensions greater than![]()
![]()
![]()
![]()
![]()
Solution?
Inverse matrices using the Gauss-Jordan elimination method
The Gauss-Jordan elimination method is quite a tedious method, but it is incomparably less tedious than trying to calculate the inverse dimensions of matrices using algebraic adjugates![]()
![]()
![]()
![]()
![]()
It is based on the use of tricks already used in Gauss’s method of solving systems of linear equations on rows – but we need to use more of them.
Attention!
In the Gauss-Jordan elimination method, we can use elementary operations only on rows. You cannot swap columns. This limitation means that in many examples it will be much more difficult for us, and often getting into fractions will be unavoidable.
Instead of a triangular matrix, we would like to obtain an identity matrix, which will require performing many more operations (and only on rows, remember). Of course, before you could learn this method, I strongly recommend thoroughly practicing the Gaussian method for solving systems of linear equations.
O.K., so how is it done?
We start with the task to calculate the matrix inverse to some given ![]()
![]()
We build a large (generally) matrix:
![]()
![]()
…where on the left side is our matrix, the inverse of which we have to calculate, and on the right side is the identity matrix (a square one with ‘ones’ on the main diagonal and only zeros outside of them). Then, using elementary operations known from Gauss’s method of solving systems of linear equations (e.g. adding rows after multiplying them by some number), we transform this large matrix into the form:
![]()
![]()
… in which the matrix B on the right side of the line is our result, i.e. the inverse matrix![]()
![]()
Easier said than done? Yes, let’s see a specific example.
Example
Let’s take a matrix![]()
![]()
![]()
![]()
![]()
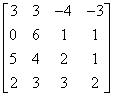
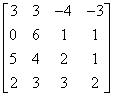
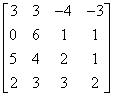
The task is to calculate its inverse matrix. We will do this using the Gauss-Jordan method. We create the appropriate matrix:
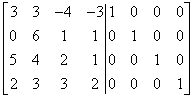
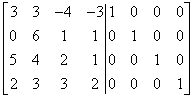
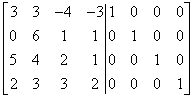
On the left side of the line there is a matrix whose inverse must be calculated, and on the right there is an identity matrix (of the appropriate dimension, of course). Our task is to reverse the situation, i.e. have an identity matrix on the left side of the line and another matrix on the right (which will be our result – by the way).
We work as we did when solving systems of linear equations using the Gaussian method, but with emphasis on having ‘1’ on the diagonal, and without changing the columns (because I can only work on rows). So I start from the first column and manipulate it so that I get ‘1’ in the right place (i.e. in the first row and first column).
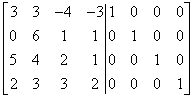
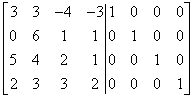
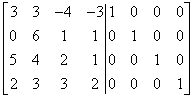
Multiply the first row by![]()
![]()
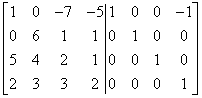
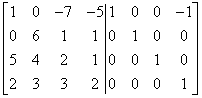
Now I zero out the first column by multiplying the first row by -5 and adding to the third:
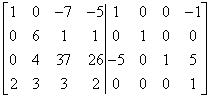
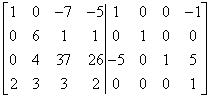
…and multiplying the first row by -2 and adding to the fourth:
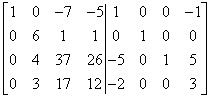
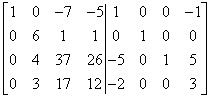
The first column is already “correct” – as it should be in the identity matrix. We go to the second one. First we need to get ‘1’ in the second row of the second column (where it should be in the identity matrix). There is ‘6’ there at the moment. Multiply second row by![]()
![]()
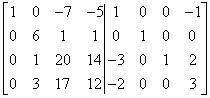
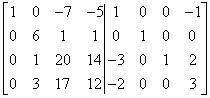
…and I have ‘1’ in the third row of the matrix (i.e. not where it needs to be yet). Now I swap the third and second rows:
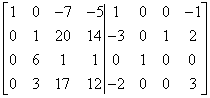
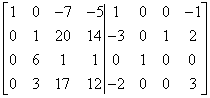
… and I have one in the right place. Now I “zero” the second column (I leave the first row alone because it already has zero there). I multiply the second row of the matrix by -6 and add it to the third:
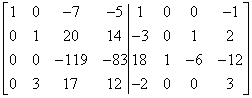
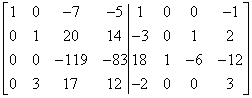
I multiply the second row of the matrix by -3 and add it to the fourth:
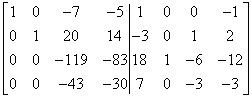
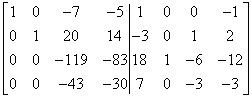
We have the second column of the matrix “zeroed”. We can move on to the third one.
A real challenge awaits us here. We have to make ‘1’ in place ‘-119’. I can only manipulate the third and fourth rows of the matrix, because if I moved the first or second row, I would spoil the already set columns.
I multiply the fourth row by -3 and add it to the third to get:
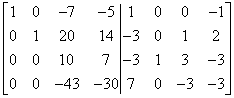
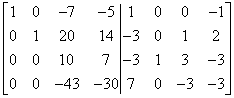
I’m fighting for ‘1’ without going further into fractions, so I’m not dividing the third line by 10. Instead, I multiply the third row by four and add it to the fourth:
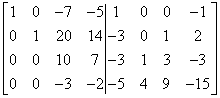
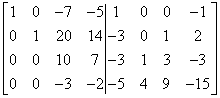
…and then I multiply the fourth by 3 and add it to the third:
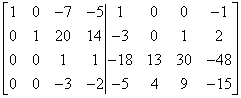
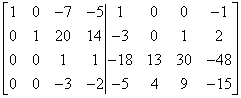
I have a grade 1 and I managed to avoid fractions, so I’m doing really well.
Now I “zero out” the ENTIRE third column (i.e. the elements of the first, second and fourth rows) by:
– multiplying the third row by 7 and adding it to the first one
– multiplying the third row by -20 and adding it to the second one
– multiplying the third row by 3 and adding it to the fourth
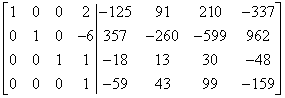
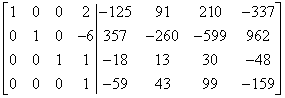
The third column is ready.
I’m moving on to fourth column.
Luckily, we already have ‘1’ in the right place in the matrix (fourth row and fourth column). If there was no 1 there, we would only have one option: divide the fourth line by the appropriate number, even if it meant creating fractions.
But luckily we can ‘zero out’ the fourth column on the spot by:
– multiplying the fourth row by -2 and adding it to the first
– multiplying the fourth row by 6 and adding it to the second one
– multiplying the fourth row by -1 and adding to the third
And this is how we reached our destination! On the left side we have the identity matrix and on the right the inverse matrix we are looking for.
Now we need to just write down the answer:
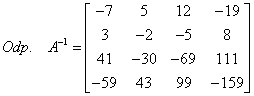
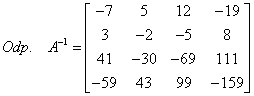
Don’t believe the answer is correct?
Test me by multiplying the matrix whose inverse we were supposed to calculate:
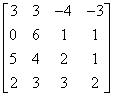
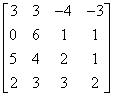
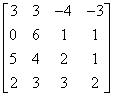
by the resulting matrix:
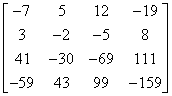
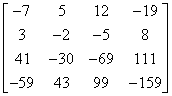
the result should be an identity matrix! 🙂
Click to remember how to use the inverse matrix to solve a system of equations (previous Lecture)< —