
Co można zrobić, gdy potęgowanie po prostu nie idzie (liczby zespolone)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Bywają takie dni, w których po prostu nic się nie udaje.
Bywają także takie przykłady z liczb zespolonych, w których nic nie idzie. Znane i wykute metody nie pomagają.
Weźmy na przykład taki sobie niewinne potęgowanie:
{( 1+2i )^8}Drepcząc wydeptaną już w wielu przykładach ścieżką chcesz zapisać liczbę ![]() w postaci trygonometrycznej i później podnieść do ósmej potęgi z odpowiedniego wzoru.
w postaci trygonometrycznej i później podnieść do ósmej potęgi z odpowiedniego wzoru.
Liczysz więc moduł:
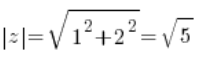
Liczysz sinusa i cosinusa argumentu głównego:
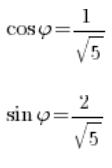
Znaki przy cosinus i sinus są na plus, zatem kąt jest z pierwszej ćwiartki, ale na tym się kończy Twoje szczęście.
Niestety wartości sinusa i cosinusa: ![]() i
i ![]() nie znajdziesz w tabelce podstawowych wartości trygonometrycznych. Nic dziwnego – kąt
nie znajdziesz w tabelce podstawowych wartości trygonometrycznych. Nic dziwnego – kąt ![]() , którym on odpowiada to nie jest kąt ani 0, ani 30, ani 45, ani 60, ani 90 stopni.
, którym on odpowiada to nie jest kąt ani 0, ani 30, ani 45, ani 60, ani 90 stopni.
Czyli PROBLEM.
Co można zrobić?
Sytuacja, w której liczba podniesiona do potęgi nie daje się tak łatwo przekształcić na postać trygonometryczną może się zdarzyć. Niestety.
Ale nikt nie powiedział, że ta sama liczba PODNIESIONA DO KWADRATU (na przykład) nadal będzie „nieprzekształacalna”.
No to spróbuj:
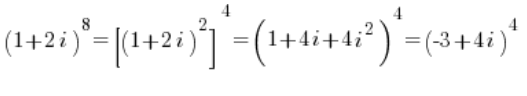
Zamiast liczby: ![]() na postać trygonometryczną przekształcasz więc liczbę
na postać trygonometryczną przekształcasz więc liczbę ![]() …
…
Niestety z równie opłakanym rezultatem, bo mimo, że moduł wyjdzie ładny i okrągły, to wartości sinusa i cosinusa nadal nie dasz rady odczytać z tabelki.
Co teraz?
Powtórz manewr 🙂
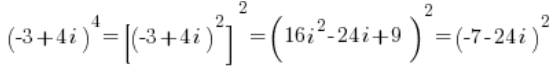
A tutaj zamiast męczyć się już w trygonometryczną, po prostu podnieś to do kwadratu w postaci algebraicznej:
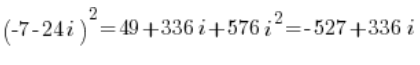
W ten oto sposób, zauważ, nie tykając właściwie postaci trygonometrycznej (bo się nie dało), dosyć – chyba jeszcze bezboleśnie – policzyliśmy w miarę wysoką potęgę liczby zespolonej:
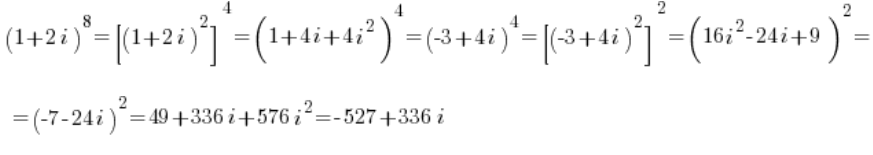
Oczywiście. To nie zawsze „zadziała”. Ale może czasami pomóc, prawda? 🙂
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Proszę o pomoc – mam takie zadanie, którego niestety w kursie brak i zupełnie nie wiem jak się za nie zabrać.
Wyznaczyć:
Szukałem tego wyjaśnienia po całym \internecie. Tak czułem, że na tej stronie je znajdę 🙂 Dzięki wielkie za objaśnienia! Kursy są bardzo pomocne i fajnie tłumaczone. Tylko właśnie tego przypadku dokładniej objaśnionego mi brakowało w Lekcji 4 liczb zespolonych. Poza tym rewelka! Pozdrawiam, wszystkiego dobrego 🙂
Witam, prosiłabym o rozwiązanie przykładu 7 i 8 z zadania domowego z podnoszenia liczb zespolonych do potęgi. Niestety nie mam pojęcia jak się za to zabrać a chciałabym te przykłady umieć zrobić, ponieważ nie mam za bardzo poglądu co będę mieć na kolokwium dlatego tak mi na tym zależy. Starałam się najpierw pomnożyć licznik i mianownik poprzez sprzężenie mianownika aczkolwiek wynik dalej nie wychodzi tak jak jest w odpowiedziach. Z góry dziękuje za pomoc.
Witam, pomoc jest już nie potrzebna. Przespałem się z tym i dziś rozwiązałem zadanie 1 i 5 bez większych kłopotów. Wynik jest prawidłowy. Dziękuję za dobry kurs.
Świetnie, to jest prawdziwa moc dobrego snu 🙂
Witam, bardzo proszę o rozwiązanie przykładu 1 i 5 z zadania domowego z podnoszenia liczb zespolonych do potęgi. Liczyłem kilka razy i przeglądałem materiał filmowy kilkukrotnie, wynik nadal nie wychodzi mi prawidłowy tj. w 1 wychodzi, ale nie zgadzają się znaki. W zadaniu piątym natomiast względem odpowiedzi zostają mi zbędne pierwiastki z dwóch w wyniku końcowym. Po wpisaniu tego działania do wolfram, wynik wyświetla prawidłowy, więc coś muszę robić nie tak, ale nie potrafię dojść co to jest.
Witam, jeśli można prosiłbym o rozwiązanie przykładu 6 z zadania domowego lekcji 4 liczb zespolonych. Liczę i liczę, a wynik nie chce wyjść taki jak powinien.
a w przykladzie a) ma byc zamiast jedynki i 🙂
przepraszam, w ostatnim zamiast (ctga+1) jest obliczyc modul z (ctga+i)
Dziękuję Panu za ten przykład !! Właśnie identyczne próby robiłam i nie dawało to rezultatu a dzięki temu zrozumiałam, że trzeba kombinować inaczej :). Chciałabym się spytać o pare innych przykładów z którymi też mam problem:
a) znaleźć rozwiązanie: sprzężenie [(2+1)^3]
b) uzadadnic tozsamosc: |z^n|=|z|^n
c) obliczyc moduły: (sin4a-icos4a)
(ctga+1)
Witam, proszę o pomoc 🙂 nie bardzo mam czas pisać w tym zautomatyzowanym jezyku Latex więc przedstawię to normalnie, wierzę że uda się to rozszyfrować
Oblicz.
sqrt z1 ^ 5 dzielone na z2
gdzie z1= cos 4π/ 25 + isin 4 π/ 25 z2=i
Pomocy!
Witam,
Hmmm… mam wątpliwości, z czego liczony jest pierwiastek (czy tylko z {{z}_{1}}^{5}, czy też z całego ułamka \frac{{{z}_{1}}^{5}}{{{z}_{2}}}).
Zaryzykuję i przyjmuję, że do policzenia ma Pan: \sqrt{\frac{{{z}_{1}}^{5}}{{{z}_{2}}}}, gdzie:
{{z}_{1}}=cos \frac{4pi }{25}+isin \frac{4pi }{25}
{{z}_{2}}=i
Liczę najpierw {{z}_{1}}^{5}(ze wzoru Moivre’a):
{{z}_{1}}^{5}={{\left( cos \frac{4pi }{25}+isin \frac{4pi }{25} \right)}^{5}}=cos \left( 5\cdot \frac{4pi }{25} \right)+isin \left( 5\cdot \frac{4pi }{25} \right)=cos \frac{4}{5}pi +isin \frac{4}{5}pi
Teraz zamieniam {{z}_{2}}na postać trygonometryczną (metodą jak w filmiku):
{{z}_{2}}=i=cos \frac{\pi }{2}+isin \frac{\pi }{2}
i dzielę {{z}_{1}}^{5}przez {{z}_{2}}(tak, jak dzieli się liczby w postaci trygonometrycznej:
\frac{{{z}_{1}}^{5}}{{{z}_{2}}}=\frac{cos \frac{4}{5}pi +isin \frac{4}{5}pi }{cos \frac{\pi }{2}+isin \frac{\pi }{2}}=cos \left( \frac{4}{5}pi -\frac{\pi }{2} \right)+isin \left( \frac{4}{5}pi -\frac{\pi }{2} \right)=cos \frac{3}{10}pi +isin \frac{3}{10}pi
Teraz już tylko liczę pierwiastki (wzorem z Lekcji 5 mojego Kursu):
{{\omega }_{0}}=cos \frac{\frac{3}{10}pi }{2}+isin \frac{\frac{3}{10}pi }{2}=cos \frac{3}{20}pi +isin \frac{3}{20}pi
{{\omega }_{1}}=cos \frac{\frac{3}{10}pi +2\pi }{2}+isin \frac{\frac{3}{10}pi +2\pi }{2}=cos \frac{\frac{13}{10}pi }{2}+isin \frac{\frac{13}{10}pi }{2}=cos \frac{13}{20}pi +isin \frac{13}{20}pi
Trochę nieciekawe te pierwiastki mi wyszły, czy na pewno dobrze odczytałem Pana zapis: „sqrt z1 ^ 5 dzielone na z2 ” ?
Tak dobrze Pan odczytał mój zapis 🙂 niestety jak to Pan mówi jestem na „mocniejszej” uczelni i wychodzą takie nieciekawe wyniki. Bardzo dziękuję za pomoc w rozwiązaniu!
No i przy potęgach do 10 można się pomęczyć z trójkątem Pascala – zawsze jakaś alternatywa! 🙂
Tak, to dobry pomysł. Albo można wykorzystać to, że: [pmath]a^10={a^8}{a^2}=(((a^2)^2)^2)a^2[/pmath] i znowu jedyne co robimy za każdym przejściem to podnosimy do kwadratu 🙂