अर्थमिति – व्याख्यान 1
विषय: अर्थमिति क्या है?
बहुत से लोगों ने मुझसे पूछा:
अर्थमिति – आखिर यह क्या होती है?
खासकर जब वे सुनते हैं कि मैं “कंप्यूटर साइंस और अर्थमिति” पढ़ रहा हूँ (हाँ, सचमुच ऐसा एक कोर्स होता है 🙂)। नाम सुनने में थोड़ा रहस्यमय लगता है, यह सच है। लेकिन जब हम इसके मूल में जाते हैं, तो अर्थमिति वाकई दिलचस्प विषय है। आप यह भी कह सकते हैं कि यह “जीवन से जुड़ी” चीज़ है — यानी जो हम इसमें सीखते हैं, उसे वास्तविक जीवन में भी इस्तेमाल कर सकते हैं।
तो फिर, अर्थमिति की यात्रा शुरू करने के लिए हमें क्या चाहिए?
एक साधारण कैलकुलेटर, कुछ बुनियादी गणितीय फ़ंक्शन की जानकारी, थोड़ी कल्पनाशक्ति और तथ्यों को जोड़ने की क्षमता। बाकी सब अपने-आप आता है।
आइए एक छोटा सा उदाहरण देखते हैं।
उदाहरण 1
कुछ छात्रों के समूह से यह पूछा गया कि उन्होंने एक महत्वपूर्ण परीक्षा (कोलोकीयम) से पहले पढ़ाई में कितना समय (घंटों में) लगाया। बाद में यह देखा गया कि उन्हें क्या ग्रेड मिले। परिणाम नीचे दी गई तालिका में दर्ज किए गए:
हम्म… केवल संख्याओं को देखना हर किसी के लिए अर्थपूर्ण नहीं होता। इसलिए, हर विशेषता (चर) के लिए अलग-अलग ग्राफ़ बनाना उपयोगी होता है — यानी प्रत्येक छात्र के लिए उसके अध्ययन समय और ग्रेड को अंकित करें।
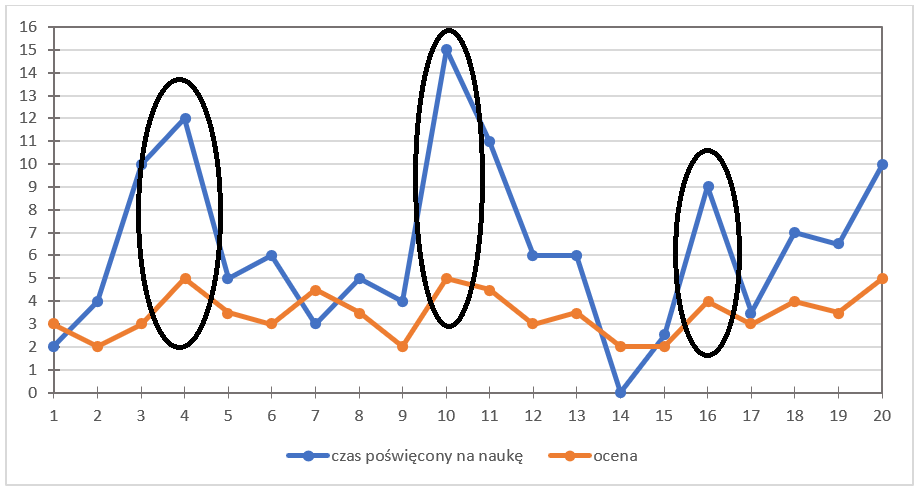
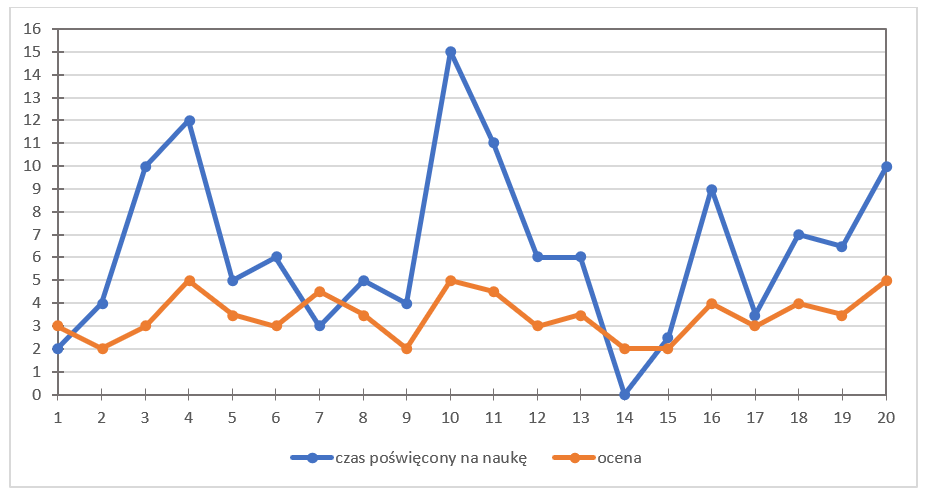
यह रहा वह ग्राफ़:
ये “लहरें” जैसी आकृतियाँ क्यों बनी हैं? X-अक्ष (OX) छात्रों की क्रम संख्या दिखाता है, जबकि Y-अक्ष (OY) ग्रेड का मान (नारंगी रेखा) और अध्ययन समय (नीली रेखा) दर्शाता है। सही बिंदुओं को अंकित करना बहुत महत्वपूर्ण है, इसलिए तालिका और ग्राफ़ को ध्यान से देखिए।
मैंने जानबूझकर दोनों ग्राफ़ को एक ही चित्र पर रखा है। क्यों? ताकि हम यह देख सकें कि ये दोनों चर (वेरिएबल्स) एक-दूसरे के संबंध में कैसे व्यवहार करते हैं। क्या अध्ययन समय और ग्रेड के बीच कोई संबंध है?
आप निश्चित रूप से देख सकते हैं कि दोनों रेखाओं में “ऊँचाइयाँ” और “गहराइयाँ” हैं। क्या ये शिखर और गर्त एक ही छात्र पर एक साथ दिखाई देते हैं?
बिलकुल सही — यह स्पष्ट रूप से दिखता है। उदाहरण के लिए, यहाँ कुछ ऊँचाइयाँ हैं:
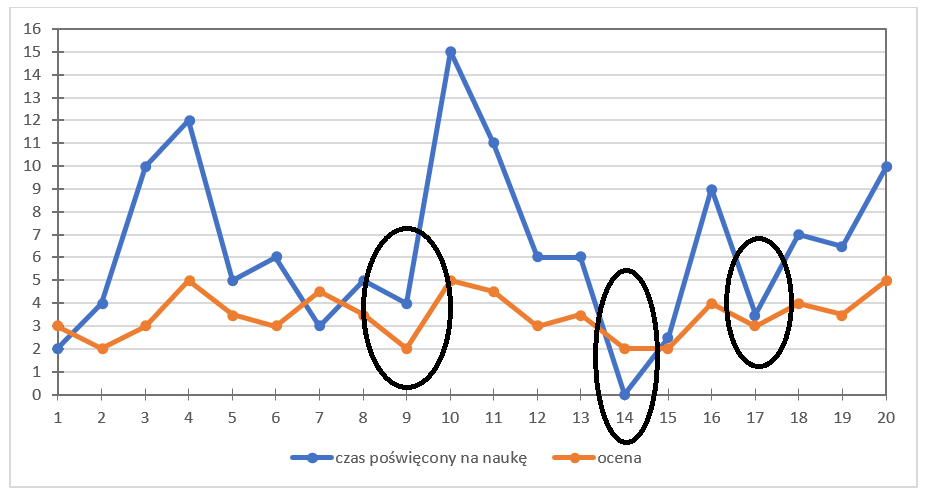
और यहाँ कुछ गहराइयाँ हैं:
जैसा कि आप देख सकते हैं, जब हम किसी वास्तविक घटना को दर्शाने वाले डेटा का विश्लेषण करते हैं (मान लें, कुछ छात्रों के लिए परीक्षा से पहले पढ़ाई करना भी “घटना” जैसा ही है 😄), तो हम उनमें कुछ संबंध पहचान सकते हैं। आप क्या सोचते हैं?
बिलकुल सही! (खासकर ग्राफ़ से देखते हुए) यह साफ़ दिखाई देता है कि जितना ज़्यादा आप पढ़ते हैं, उतना बेहतर और ऊँचा ग्रेड मिलता है — और उल्टा भी सही है। आम तौर पर यह बात बिल्कुल सही होती है, हालांकि हर नियम के कुछ अपवाद भी होते हैं। (मुझे एक मज़ेदार कहावत याद आई: “2 के लिए पढ़ा, 3 की उम्मीद की, 4 मिला, और सोचते रह गए — 5 क्यों नहीं मिला!” 😄)
ठीक है, अब जब हमने यह समझ लिया कि इन दो विशेषताओं के बीच कुछ संबंध है, तो आइए इन आंकड़ों के लिए एक और ग्राफ़ बनाते हैं — इस बार अध्ययन समय को ग्रेड पर निर्भर करते हुए दिखाते हैं। यानी, इस बार हम निर्देशांक प्रणाली में छात्र की संख्या नहीं, बल्कि केवल दो विशेषताओं को दिखाएँगे:
मान लें कि अध्ययन समय हमारा X (स्वतंत्र चर) है, और प्राप्त ग्रेड Y (निर्भर चर) है। इससे हमें निम्नलिखित बिंदु मिलते हैं:
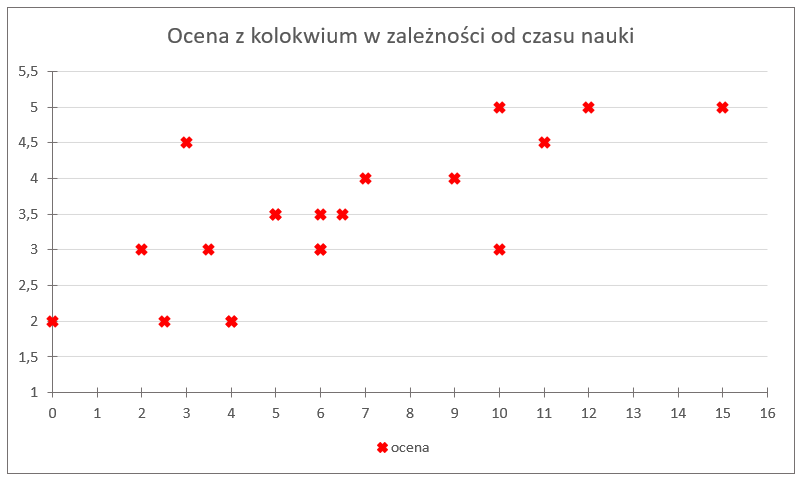
जैसा कि आप देख सकते हैं, इन सभी बिंदुओं को एक ही टूटी हुई रेखा में जोड़ना मुश्किल है — यह संभव नहीं है। लेकिन ये बिंदु एक “बादल” जैसे पैटर्न में व्यवस्थित हैं, ज़रा देखिए:
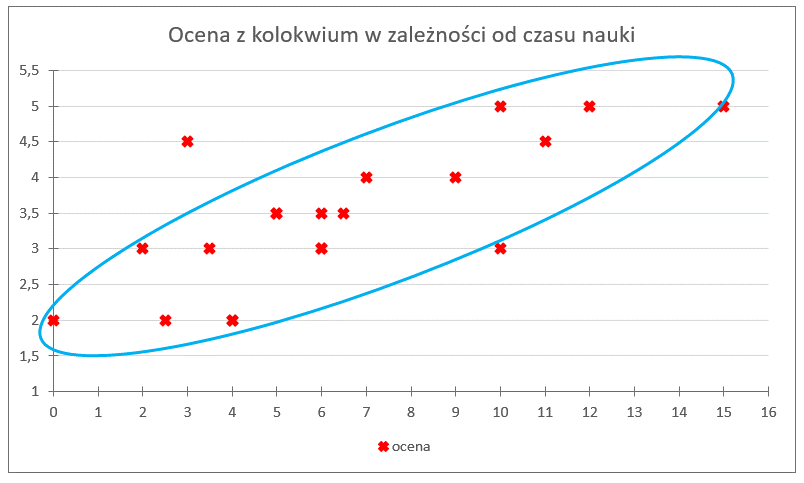
आप इस आकृति के बारे में क्या कहेंगे? इसका झुकाव क्या दर्शाता है?
स्पष्ट है कि यह आकृति “सुंदर”, लम्बी और ऊपर की ओर झुकी हुई है। यानी हमारी पहले देखी गई प्रवृत्ति (जितना अधिक अध्ययन समय, उतना बेहतर ग्रेड) यहाँ भी स्पष्ट रूप से दिखाई दे रही है। आकृति से हम यह भी कह सकते हैं कि यह रेखीय प्रकृति की है — यानी यह लगभग एक ऊपर जाती सीधी रेखा के समान है जो इस पूरे बिंदु-बादल को समेटती है।
इससे यह साबित होता है कि इन दो विशेषताओं के बीच का संबंध गणितीय रूप से व्यक्त किया जा सकता है। है न दिलचस्प?
बेशक, यह याद रखना चाहिए कि यह संबंध का सटीक वर्णन नहीं है, बल्कि एक अनुमानित फ़ंक्शन है जो उस संबंध को सबसे अच्छे तरीके से दर्शाने की कोशिश करता है। इस उदाहरण में, यह एक सीधी रेखा — यानी रेखीय फ़ंक्शन — जैसा दिखता है।
अब जब हमने यह निर्धारित कर लिया है कि अधिकांश बिंदु एक ही फ़ंक्शन से वर्णित किए जा सकते हैं, तो हम कह सकते हैं कि यह संबंध मापा जा सकता है। अब सवाल है — उस फ़ंक्शन को कैसे बनाया जाए, कैसे गणना की जाए, और यह हमें किस काम आएगा?
यहीं पर अर्थमिति काम में आती है!
अर्थमिति की परिभाषा
बीसवीं सदी की शुरुआत में, एक पोलिश वैज्ञानिक ने दो ग्रीक शब्दों को मिलाया — oikonomia (जिसका अर्थ है “प्रशासन” या “अर्थव्यवस्था”) और metron (जिसका अर्थ है “मापन”) — और एक नया शब्द बनाया: अर्थमिति (Econometrics)। शाब्दिक अर्थ में, इसका मतलब है “अर्थव्यवस्था का मापन”।
कुल मिलाकर यह काफ़ी तार्किक लगता है 🙂 क्योंकि यही तो मूल रूप से अर्थमिति का उद्देश्य है — गणितीय और सांख्यिकीय विधियों की सहायता से आर्थिक घटनाओं में मौजूद नियमितताओं (नियमों) को मापना। सरल शब्दों में, अर्थमिति यह बताती है कि एक चर (variable) का व्यवहार दूसरे चरों के व्यवहार पर कैसे निर्भर करता है।
इसलिए यहाँ केवल गणित ही नहीं, बल्कि सांख्यिकी भी महत्वपूर्ण भूमिका निभाती है। डेटा मनगढ़ंत नहीं होना चाहिए, बल्कि वास्तविक होना चाहिए। जिन आंकड़ों को इकट्ठा कर दर्ज किया जाता है, उन्हें सांख्यिकीय डेटा कहा जाता है। इसीलिए अर्थमिति को सांख्यिकी का “स्वाभाविक बच्चा” भी कहा जाता है 🙂।
अब अपने उदाहरण पर वापस आते हैं। हमने देखा कि वास्तविक, “जीवन से जुड़े” चरों के बीच कुछ संबंध है — इसलिए हम यह कह सकते हैं कि आर्थिक चरों के बीच भी ऐसे संबंध मौजूद होते हैं।
मान लें कि अब एक और छात्र — क्रमांक 21 — अपने साथियों के डेटा का विश्लेषण करके यह “गणना” करना चाहता है कि उसे किसी विशेष ग्रेड (मान लीजिए, 3 या 3.5) पाने के लिए लगभग कितना समय पढ़ाई में लगाना चाहिए। या फिर, यदि वह आधा दिन पढ़े, तो उसे किस ग्रेड की उम्मीद करनी चाहिए?
इन सवालों के जवाब देने के लिए, यानी “गणना” करने के लिए, हमें एक ठोस समीकरण की आवश्यकता है। यहीं आता है अगला सिद्धांत — अर्थमितीय मॉडल (Econometric Model)।
अर्थमितीय मॉडल की परिभाषा
अर्थमितीय विश्लेषण में सबसे महत्वपूर्ण उपकरण अर्थमितीय मॉडल होता है। (और नहीं, यहाँ “मॉडल” का मतलब फैशन मॉडल से नहीं है 😄) — यह एक औपचारिक सैद्धांतिक संरचना है जो किसी वास्तविक आर्थिक घटना का प्रतिनिधित्व करती है ताकि उसे बेहतर ढंग से समझा जा सके। यह एक या अधिक समीकरणों के माध्यम से उन चरों के बीच संबंध दर्शाती है जिन्हें हमने चुना है। इस प्रकार यह एक गणितीय मॉडल है जिसे सांख्यिकीय विधियों की सहायता से वास्तविकता के अनुरूप “फिट” किया गया है।
ध्यान रखें कि यह मॉडल हमेशा वास्तविकता का एक सरलीकृत रूप होता है — जैसे एक हवाई जहाज का मॉडल या DNA के सर्पिल का मॉडल। यह वास्तविक दुनिया में मौजूद किसी चीज़ को “चित्रात्मक रूप” में दर्शाता है। अर्थमितीय मॉडल केवल वास्तविकता के सबसे महत्वपूर्ण तत्वों को शामिल करता है और कम महत्वपूर्ण कारकों को नज़रअंदाज़ करता है। आप शायद मुझसे सहमत होंगे कि सभी संभावनाओं को ध्यान में लेना असंभव है 🙂।
औपचारिक रूप से, मॉडल को एक समीकरण के रूप में व्यक्त किया जाता है। इसका सामान्य रूप इस प्रकार है:
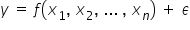
ऐसे मॉडल में कुछ मुख्य घटक होते हैं:
पहला — चर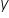 
— यह वह चर है जिसका व्यवहार आप मॉडल की सहायता से समझाना चाहते हैं। इसलिए इसे निर्भर चर (Dependent Variable) या व्याख्यायित चर कहा जाता है।
चर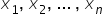 
अगली n व्याख्यात्मक (स्वतंत्र) चर हैं। ये वही चर हैं जिनकी मदद से हम निर्भर चर को समझाते हैं। कभी-कभी केवल एक ही व्याख्यात्मक चर काफ़ी होता है। स्वाभाविक रूप से, इनकी स्पष्ट आर्थिक व्याख्या होनी चाहिए।
फ़ंक्शन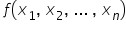 
निर्भर चर और व्याख्यात्मक चरों के बीच कार्यात्मक संबंध का लेखा-जोखा देता है, और इसमें एक यादृच्छिक घटक भी शामिल होता है।
हाँ, वही रहस्यमय अक्षर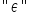 
— यह ग्रीक अक्षर एप्सिलॉन (ε) है। यह तथाकथित यादृच्छिक घटक/त्रुटि पद को दर्शाता है। इसके बारे में दो बातें:
यादृच्छिक घटक मॉडल में अन्य कारकों से उत्पन्न “व्यवधान” को दर्शाता है। गणितीय समीकरण हमेशा वास्तविकता का एक सन्निकटन होते हैं। इसलिए यह घटक, अन्य बातों के अलावा, इन बातों का हिसाब रखता है: मॉडल और वास्तविकता के बीच का अंतर; उन अन्य चरों का प्रभाव जो मॉडल में शामिल नहीं हैं; माप-त्रुटियाँ; और विविध आकस्मिक/अनपेक्षित कारक।
उफ़्फ़, काफ़ी सिद्धांत हो गया 🙂
अब अपने उदाहरण पर लौटते हैं। हमने तय किया कि इन दो विशेषताओं के बीच रेखीय संबंध है। यहाँ हमें मिडिल स्कूल की याद आती है—रेखीय फ़ंक्शन का सूत्र कैसा था?
वह इस तरह था: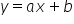 
।
यहाँ चरों को बस एक-दूसरे में जोड़ा जाता है और उपयुक्त स्केलरों—यानी पैरामीटर (a, b)—से गुणा किया जाता है। तो क्या यही हमारा मॉडल है?
जवाब है—लगभग हाँ 🙂
लिखा हुआ यह समीकरण सैद्धांतिक मॉडल का रूप है। इसे सामान्य मॉडल से प्रतीकात्मक रूप से अलग दिखाने के लिए y के ऊपर “टोपी” (हैट) लगाते हैं। तब समीकरण
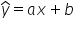
को हम सैद्धांतिक अर्थमितीय मॉडल मानते हैं।
बुरा नहीं किया, है ना? 🙂
अब यह सामान्य रूप में कैसा दिखेगा—यानि सब कुछ सम्मिलित करते हुए, उन उपेक्षित और कम महत्वपूर्ण चरों सहित? इस प्रकार:
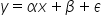
यह एक व्याख्यात्मक चर के लिए है। और कई चरों के लिए:
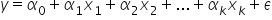
औपचारिक लेखन में प्रायः पैरामीटरों के लिए क्रमिक ग्रीक अक्षरों (α, β, इत्यादि) का उपयोग किया जाता है—जिन्हें बाद में संख्यात्मक रूप से आँका/मापा जाता है।
हमारे उदाहरण में हमने ग्रेड (कोलोकीयम की अंक) को अध्ययन-समय पर निर्भर माना। क्या संबंध उल्टा होना चाहिए—यानी अध्ययन-समय ग्रेड पर निर्भर? तब हम ऐसे मॉडल पर विचार कर सकते हैं:
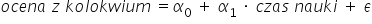
या फिर ऐसा:
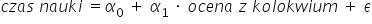
यहाँ हमें अपनी तर्कसंगत समझ और कारण-परिणाम संबंधों का ज्ञान काम आता है। साफ़ है कि दूसरा मॉडल अर्थहीन है—क्योंकि भला कौन अध्ययन-समय को तब “मापेगा” जब ग्रेड पहले ही मिल चुका हो? 🙂
अतः सामान्य मॉडल इस रूप में होगा: ।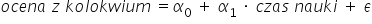
तो फिर इस “एप्सिलॉन” के भीतर क्या छिपा है?
अन्य वे चर जिन्हें हम मॉडल में शामिल नहीं कर रहे हैं—जैसे, व्याख्यान में उपस्थिति की संख्या, अध्यापक का उस दिन का मूड वगैरह। कुछ छिपे हुए यादृच्छिक कारक भी होते हैं, जैसे छात्र का अचानक बीमार पड़ जाना—बहुत पढ़ने के बावजूद कमजोरी और एकाग्रता में कमी के कारण ग्रेड कम आ जाना।
अब अर्थमिति का काम है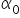 
और 
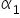के उपयुक्त मानों का आकलन करना। तब हमें पैरामीटरों के संख्यात्मक—अर्थात् अनुमानित—मान मिलेंगे, जिन्हें प्रायः 
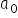और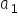 
से दर्शाया जाता है, या किसी की पसंद के अनुसार क्रमशः 
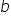और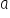 
लिखा जाता है। उदाहरण के लिए:
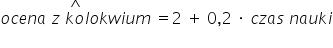
इन संख्यात्मक मानों की गणना कैसे की जाती है, यह एक अलग विषय है 🙂
विधियाँ कई हैं, और प्रत्येक के प्रयोग की अपनी शर्तें होती हैं। हमारे इस विशिष्ट मॉडल में हमने रैखिक (linear) संबंध माना है—जिसका सत्यापन और उपयोग सबसे सरल है।
स्वाभाविक रूप से, जो फ़ंक्शन 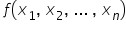व्याख्यात्मक चरों के बीच संबंध दर्शाता है, वह किसी भी रूप का हो सकता है—घातीय (exponential), लघुगणकीय (logarithmic), परिमेय (rational) इत्यादि—या इनका मिश्रण भी। अब हमें बस यह जाँचना है कि मॉडल अच्छा है या नहीं (क्या यह आवश्यक मान्यताओं को पूरा करता है), फिर कुछ निष्कर्ष निकालकर उसे लागू करना है—जैसे, छात्र संख्या 21 के लिए इच्छित मानों की गणना करना।
देखा आपने—अर्थमिति बिल्कुल नीरस विषय नहीं है। हाँ, गणनाएँ काफ़ी होती हैं—कई अंक, सूत्र और प्रक्रियाएँ (जैसा कि सांख्यिकी में होता ही है)। लेकिन यदि आप ठीक-से सोचें कि आप क्या समझाना चाहते हैं, और उन उपयुक्त व्याख्यात्मक चरों का चुनाव करें जिन पर वह घटना निर्भर करती है (ज़रूरी नहीं कि केवल एक ही हो—निश्चिंत होकर एक से अधिक चुनिए 🙂), तो आप रिश्तों की तीव्रता और दिशा दोनों का अनुमान लगा पाएँगे, और व्यावहारिक रूप से “नए” मान भी निकाल सकेंगे।
नतीजे आपको चकित कर सकते हैं! 🙂
समाप्त
यह जानने के लिए क्लिक करें कि अर्थमितीय मॉडल क्या होता है (अगला व्याख्यान) →
अर्थमिति व्याख्यान सूची पर लौटें
