एक दीर्घवृत्त की आयतन (लेकिन घूर्णन वाली नहीं, बल्कि जंगली प्रकार की) निश्चित समाकलन द्वारा गणना की गई

---

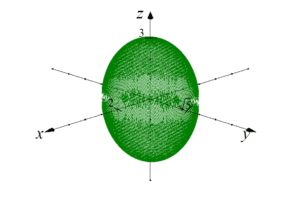
मान लीजिए हमें एक दीर्घवृत्त की आयतन गणना करनी है:

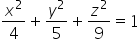
यह एक दीर्घवृत्त है जो x, y, z अक्षों को 2, और 3 पर काटता है (दीर्घवृत्त का सामान्य समीकरण है: 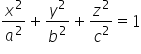, जहां a, b, c काटने के निर्देशांक हैं).

यह एक घूर्णन दीर्घवृत्त नहीं है, यह किसी भी वक्र को किसी भी अक्ष के चारों ओर घुमाकर नहीं बनता है, हम घूर्णन निकाय की आयतन के मानक सूत्र का उपयोग नहीं कर सकते:

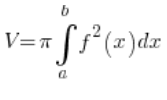
हमें कुछ और सोचना होगा।

1. दीर्घवृत्त के केंद्र में और OZ अक्ष पर किसी भी बिंदु M(z) को चुनें।

इस बिंदु से होकर गुजरने वाला और OZ अक्ष के लम्बवत स्थित तल हमें दीर्घवृत्त से एक विशेष अण्डाकार काट देता है:

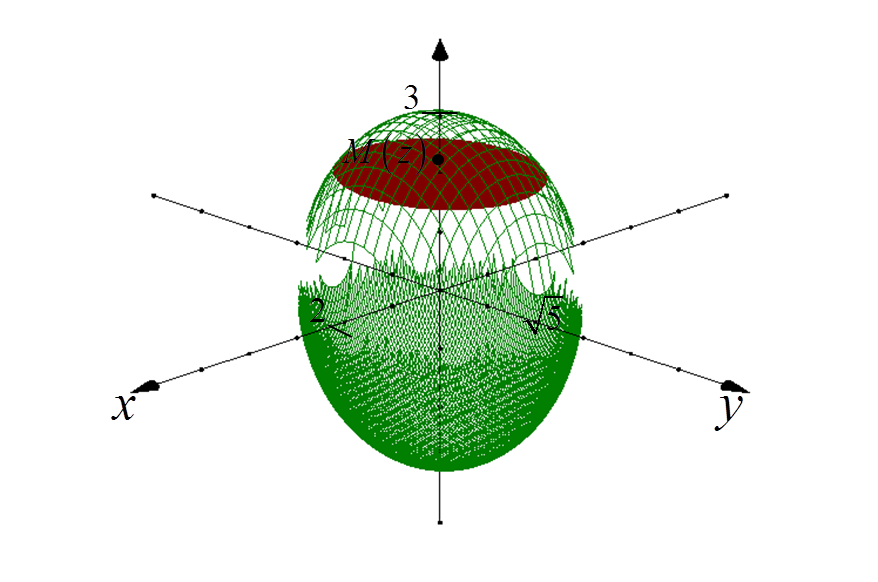
2. XY तल पर ‘काटी गई’ अण्डाकार के प्रक्षेपण का समीकरण निकालें

हम इस अण्डाकार का समीकरण निकालते हैं, निश्चित ‘z’ के लिए (हम ‘z’ को स्थिर मानते हैं) दीर्घवृत्त के सामान्य समीकरण से:

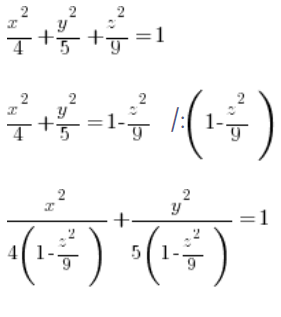
आप देख सकते हैं कि हमारे ‘a’ और ‘b’ दीर्घवृत्त के सामान्य समीकरण (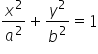) से हैं:

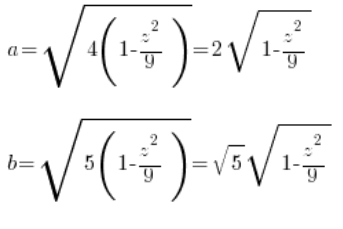
4. ‘z’ चर के आधार पर इस कटाव का क्षेत्रफल निकालें

इस अण्डाकार का क्षेत्रफल चुने गए ‘z’ बिंदु पर निर्भर करता है, इसलिए यह ‘z’ चर का एक प्रकार का फलन होगा। हम इसे या तो अण्डाकार के क्षेत्रफल के तैयार सूत्र का उपयोग करके निकाल सकते हैं ():

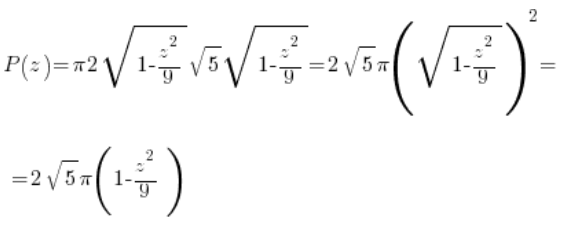
या उचित निश्चित समाकलन का मेहनत से गणना करके (बिल्कुल, अण्डाकार के पारामेट्रिक रूप और सूत्र का उपयोग करके समाकलन का क्षेत्रफल निकाल सकते हैं):

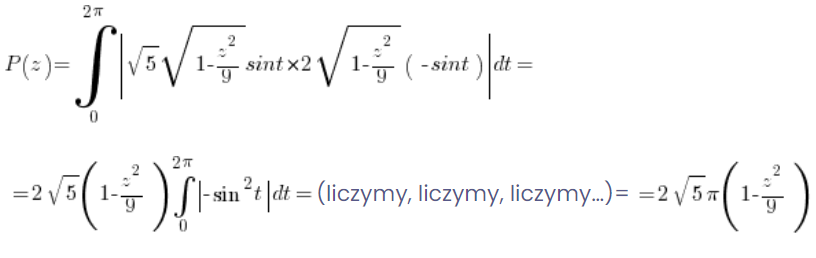
5. कटाव क्षेत्रफल का उपयोग करके निकाय का आयतन निकालें

अब मुश्किल हिस्सा आता है। निकाय का आयतन बराबर होता है – यह थोड़ा अजीब लगता है – सभी कटाव का “योग” (अर्थात, समाकलन), जो सामान्यतः:

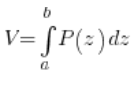
जहां Oज़ अक्ष के लंबवत तल के निकाय के कटाव का फलन है, और ‘a’ और ‘b’ वे सीमाएं हैं, जिनके भीतर ‘z’ बदलता है।

हमारे मामले में:

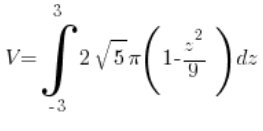= (गणना करो, गणना करो, गणना करो…) =

यह दीर्घवृत्त के सामान्य सूत्र से मेल खाता है ().

अंत

इस सामान्य योजना को याद रखना महत्वपूर्ण है, और सबसे महत्वपूर्ण बात यह है कि कठिन, गैर-घूर्णन निकाय का आयतन उनके कटाव क्षेत्रफल के फलन का समाकलन करके निकाला जा सकता है।