चौथे दर्जे के कुछ समीकरणों को द्विघात समीकरणों में सरल बनाना
कई चौथे दर्जे के बहुपद समीकरणों को हाई स्कूल में सिखाए गए एक प्रसिद्ध तरकीब का उपयोग करके द्विघात समीकरणों में बदला जा सकता है, जैसा यहाँ वर्णित है:
यह विधि निश्चित रूप से समिश्र संख्याओं के बहुपदों के लिए भी लागू होती है।
याद दिलाने के लिए, हमारे पास समीकरण है:
{{z}^{4}}+3{{z}^{2}}+2=0हम प्रतिस्थापित करते हैं: {{z}^{2}}=t
और हमें द्विघात समीकरण मिलता है:
{{t}^{2}}+3{t}+2=0फिर हम इसे सामान्य डेल्टा का उपयोग करके हल करते हैं और इसी तरह, हमें समाधान मिलते हैं ![]() , यह याद रखते हुए कि
, यह याद रखते हुए कि ![]() हम उनसे दो नए समीकरण बनाते हैं:
हम उनसे दो नए समीकरण बनाते हैं:
![]() या
या ![]()
हम उन्हें हल करते हैं और हमारे पास चार समाधान होते हैं: ![]() ।
।
उच्च दर्जे के कुछ समीकरणों को द्विघात समीकरणों में सरल बनाना
इस विधि को 4 से अधिक दर्जे के समीकरणों पर विस्तारित करने में कोई बाधा नहीं है (बशर्ते कि वे प्रतिस्थापन के माध्यम से द्विघात में सरल किए जा सकें)।
तो हमारे पास है:
2{{z}^{6}}-5{{z}^{3}}+4=0यह भी देखा जा सकता है कि यह समतुल्य है:
2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0और प्रतिस्थापन के बाद: ![]()
हमें द्विघात समीकरण मिलता है:
2{{t}^{2}}-5t+4=0समीकरण में:
{{x}^{10}}-3{{x}^{5}}+1=0प्रतिस्थापन के बाद: ![]()
हमारे पास है:
{{t}^{2}}-3t+1=0और इसी तरह, और इसी तरह…
उदाहरण
हम समीकरण लेते हैं:
z^6+(1-i)z^3-i=0हम प्रतिस्थापित करते हैं z^2=t और हमारे पास है:
t^2+(1-i)t-i=0फिर हम गणना करते हैं:
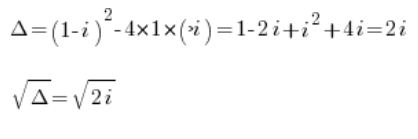
हम इन मूलों की गणना समिश्र संख्याओं की ज्ञात विधियों का उपयोग करके करते हैं (उदाहरण के लिए मेरे कोर्स में दिखाया गया है)।
हमारे पास है ![]() या
या ![]()
अर्थात:
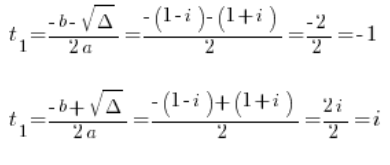
यह याद रखते हुए कि ये अभी समाधान नहीं हैं, क्योंकि z^3=t
तो हमें समीकरण हल करने हैं:
z^3=-1और:
z^3=iहम उन्हें परिवर्तित करते हैं:
![]() और
और ![]()
और ज्ञात विधियों का उपयोग करके पुनः गणना करते हुए, हमारे पास पहले समीकरण से तीन मूल हैं:
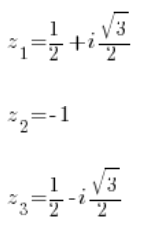
और दूसरे समीकरण से तीन मूल हैं:
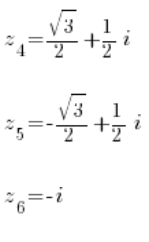
हल हो गया 🙂


