No products in the cart.
Krystian Karczyński- 24 जुलाई 2024
- Komentarz 0
यह पोस्ट उपरोक्त YouTube वीडियो पर टिप्पणी में एक सवाल के जवाब के रूप में है ( टिप्पणी का लिंक ):
मुझे कुछ समझ में नहीं आ रहा है और मुझे समझाने की ज़रूरत है, तुम “n” को क्यों कम कर रहे हो? मेरा मतलब है कि n/n एक अनिश्चित प्रतीक है (अनंत पर अनंत) मदद करो क्योंकि मैं इस पर खो गया हूँ
समझना कि वास्तव में अनिश्चित प्रतीक क्या हैं, काफी परेशानी भरा हो सकता है। इसके अलावा यह भी कई सवाल उठाता है कि इनसे “क्या किया जा सकता है” और “क्या नहीं किया जा सकता है”।
थोड़ा पुनरावलोकन
पहले इन्हें याद कर लें:
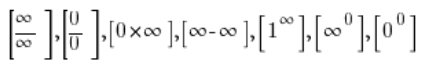
जैसा कि आपने अनिश्चित प्रतीकों में कई बार सुना होगा:
– प्रतीक 
यहाँ किसी “संख्या” या किसी गणितीय वस्तु का प्रतिनिधित्व नहीं करता है, बल्कि यह अनंतता तक बढ़ने का प्रतीक है (अनंतता संख्या नहीं है!)
– प्रतीक 
संख्या का प्रतिनिधित्व नहीं करता है, बल्कि यह शून्य तक घटने का प्रतीक है
– प्रतीक 
संख्या का प्रतिनिधित्व नहीं करता है, बल्कि यह 1 तक घटने का प्रतीक है
– अनिश्चित प्रतीक 
किसी “संख्या” को किसी “संख्या” से विभाजित करने का प्रतिनिधित्व नहीं करता है, बल्कि यह स्थिति को दर्शाता है जहाँ अंश और हर बढ़ते हुए अनंत तक बढ़ते हैं
– आदि।
इसलिए, जब हमें सीमा की गणना करनी होती है:
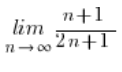
…हम कह सकते हैं कि हमारे पास अनिश्चित प्रतीक है , क्योंकि अभिव्यक्ति में अंश और हर 
तक बढ़ रहे हैं।
अभिव्यक्ति में हम अनंत को “कम” नहीं कर सकते, क्योंकि अनिश्चित अभिव्यक्ति में वे संख्या का प्रतिनिधित्व नहीं करते जो “कम” की जा सकती हैं, उन पर क्रियाएँ की जा सकती हैं आदि।
अभिव्यक्ति 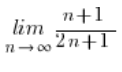में भी हम शुरुआत में कुछ “कम” नहीं कर सकते, लेकिन औपचारिक कारणों से नहीं – बल्कि बस इसलिए, क्योंकि कुछ भी कम नहीं होता है 🙂
इसलिए हमें कुछ विधियों का उपयोग करना होगा (इस मामले में, आम कारक को बाहर निकालना – जो मैंने अपने सीमा पाठ्यक्रम में वर्णित किया है), कुछ युक्तियों को अपनाना होगा, आदि।
लेकिन एक तुच्छ सीमा लें:
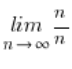
यह वास्तव में एक सीमा भी है, जिसमें हमारे पास अनिश्चित प्रतीक है – क्योंकि अंश और हर अनंत तक बढ़ रहे हैं।
अभिव्यक्ति में हम अनंत को “कम” नहीं कर सकते, लेकिन इस बार…
हम अभिव्यक्ति 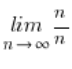में संक्षिप्तीकरण कर सकते हैं और यह पूरी तरह से संभव है।
‘n’ वास्तव में एक गणितीय चर है, जिस पर अंकगणितीय क्रियाएँ की जा सकती हैं, इसे संक्षिप्त किया जा सकता है, आदि (चिह्न के विपरीत)। तो 
और सब कुछ साफ और कानूनी है।
संक्षेप में
अनिश्चित प्रतीकों 
पर अंकगणितीय क्रियाएँ नहीं की जा सकती हैं, उन्हें संक्षिप्त नहीं किया जा सकता है, आदि।
उन अभिव्यक्तियों पर, जिनसे हम क्रम और कार्यों की सीमाएँ निकालते हैं, गणितीय क्रियाएँ की जा सकती हैं, उन्हें संक्षिप्त किया जा सकता है, आदि 
।
मुझे उम्मीद है कि मैंने आपको और अधिक भ्रमित नहीं किया है, सीमाओं के साथ शुभकामनाएँ!
