स्थान और समय
दिशात्मक अवकलज की गणना करने का विषय (यानी पास करने के लिए) वास्तव में कई चर के कार्यों के आंशिक अवकलज के तुरंत बाद आता है, जिसे अधिकांश छात्र दूसरे सेमेस्टर में पढ़ते हैं।
यह एक ऐसा विषय है जिसे शायद ही कभी लिया जाता है, इसलिए मैंने इसे अपने आंशिक अवकलज पाठ्यक्रम में शामिल नहीं किया, लेकिन यह इतना आम है कि मैं इसे ब्लॉग पर डालूंगा – उनके लाभ के लिए जिन्हें दिशात्मक अवकलज सीखना है और उनके लिए जो बस यह जानने के लिए उत्सुक हैं कि यह क्या है। हालांकि, पाठ्यक्रमों की तरह, मैं आज लगभग पूरी तरह से व्यावहारिकता पर ध्यान केंद्रित करूंगा (“मुझे यह कैसे करना है?”), न कि सिद्धांत पर (“मैं वास्तव में क्या कर रहा हूँ?”)।
दिशात्मक अवकलज – मुझे यह कैसे करना है?
दिशात्मक अवकलज के मामले में, हम x और y तर्कों की एक साथ वृद्धि से निपट रहे हैं, जो निश्चित रूप से फ़ंक्शन मान में वृद्धि के अनुरूप है 
.
कार्य के लिए हमें तीन चीजों की आवश्यकता है:
- वह फ़ंक्शन जिससे हम दिशात्मक अवकलज की गणना करेंगे।
- वह बिंदु जिस पर हम दिशात्मक अवकलज की गणना करेंगे।
- वेक्टर के रूप में दिया गया दिशा।
उपरोक्त के साथ, कार्य वेक्टर को दिशात्मक वेक्टर में बदलने पर आ जाता है (एनालिटिकल ज्यामिति की कुछ चीज़ें, मैं दिखाऊंगा कि यह कैसे करना है), और फिर इसे सूत्र में डालने का कार्य:
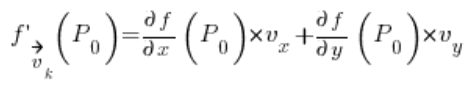
जिसमें:
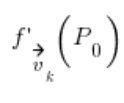बिंदु 
पर दिशात्मक अवकलज है वेक्टर 
की दिशा में
वह बिंदु है जिस पर हम दिशात्मक अवकलज की गणना करते हैं
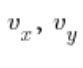दिशात्मक वेक्टर के निर्देशांक हैं
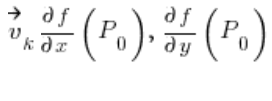फ़ंक्शन के आंशिक अवकलज हैं बिंदु पर।
फ़ंक्शन का दिशात्मक अवकलज गणना करें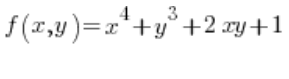 
बिंदु P(1,2) पर दिशा में 
।
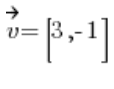समाधान:
सब कुछ तैयार है, हमें बस वेक्टर 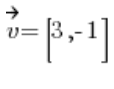को दिशात्मक वेक्टर में बदलना है।
दिशात्मक वेक्टर एक वेक्टर है जिसमें समान दिशा (कौन सोचता), समान ओरिएंटेशन, लेकिन लंबाई 1 होती है।
इसे सूत्र से गणना किया जाता है:
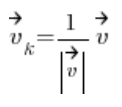
सरल शब्दों में, उसकी निर्देशांक को उसकी लंबाई से विभाजित करें।
इसलिए हम वेक्टर की लंबाई की गणना करते हैं :
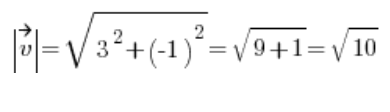
फिर हमें दिशात्मक वेक्टर मिलता है:
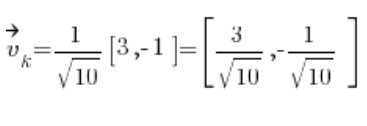
दिशात्मक अवकलज के सूत्र के लिए, हमें फ़ंक्शन के आंशिक अवकलज की भी आवश्यकता होगी 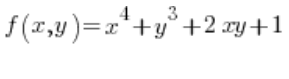बिंदु P(1,2) पर:
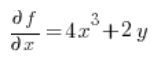
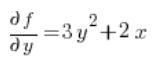
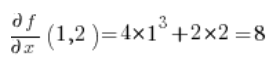
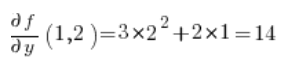
और अब हमारे पास सूत्र के लिए आवश्यक सब कुछ है:
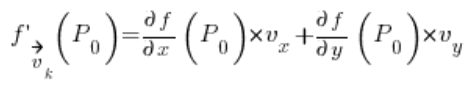
बस डालें, और हमें परिणाम मिलता है: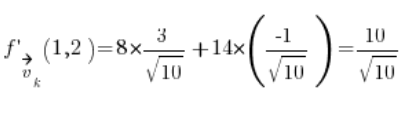 
।
हो गया।
उदाहरण 2
फंक्शन का दिशात्मक अवकलज खोजें: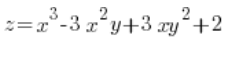 
बिंदु P(3,1) पर इस बिंदु से बिंदु Q(6,5) की दिशा में।
समाधान:
कार्य थोड़ा कठिन है क्योंकि दिशात्मक वेक्टर सीधे नहीं दिया गया है, लेकिन कोई बात नहीं।
हम बिंदु P से बिंदु Q की ओर बढ़ते हैं, इसलिए स्थानांतरण वेक्टर [3,4] है।
अब हम वेक्टर [3,4] की लंबाई की गणना करके दिशात्मक वेक्टर खोजते हैं:
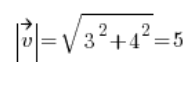
और हमें दिशात्मक वेक्टर मिलता है:
अब हम बिंदु (3,1) पर आंशिक अवकलज की गणना करते हैं:
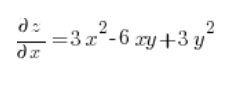
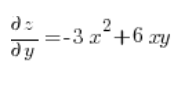
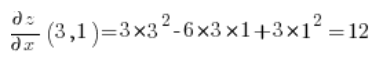
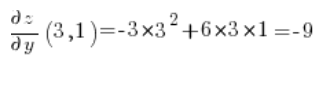
फिर हम बस दिशात्मक अवकलज के सूत्र में डालते हैं:
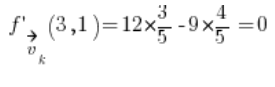
उदाहरण 3
फंक्शन का दिशात्मक अवकलज खोजें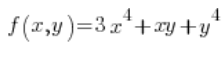 
बिंदु (1,2) पर उस दिशा में जो सकारात्मक x-अक्ष के साथ कोण 
बनाता है।
समाधान:
कार्य अधिक कठिन लगता है, क्योंकि डेटा में दिशात्मक वेक्टर की कमी है। चलो पूरी चीज़ को चित्रित करें:
मुद्दा यह है कि निर्दिष्ट दिशा में किसी भी वेक्टर के निर्देशांक को खोजना है।
हम इसका उपयोग करते हैं कि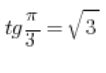 
और हम मान सकते हैं कि हमारे वेक्टर का निर्देशांक है 
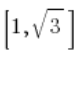, जैसा कि चित्र में है (लाइन की दिशा में किसी भी वेक्टर को चुनना पर्याप्त था):
और अब हम पुरानी विधि का अनुसरण करते हैं।
हम दिशात्मक वेक्टर की गणना करते हैं:
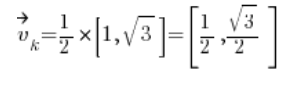
फिर बिंदु (1,2) पर आंशिक अवकलज:
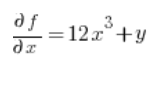
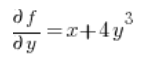
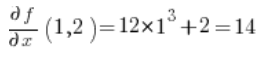
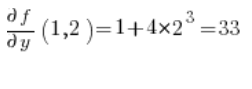
सूत्र में डालें, और हमें परिणाम मिलता है
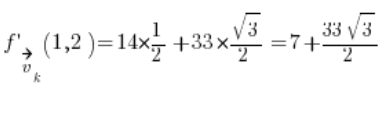
टिप्पणियों में प्रश्न पूछने के लिए आपका स्वागत है – हमेशा की तरह 🙂
