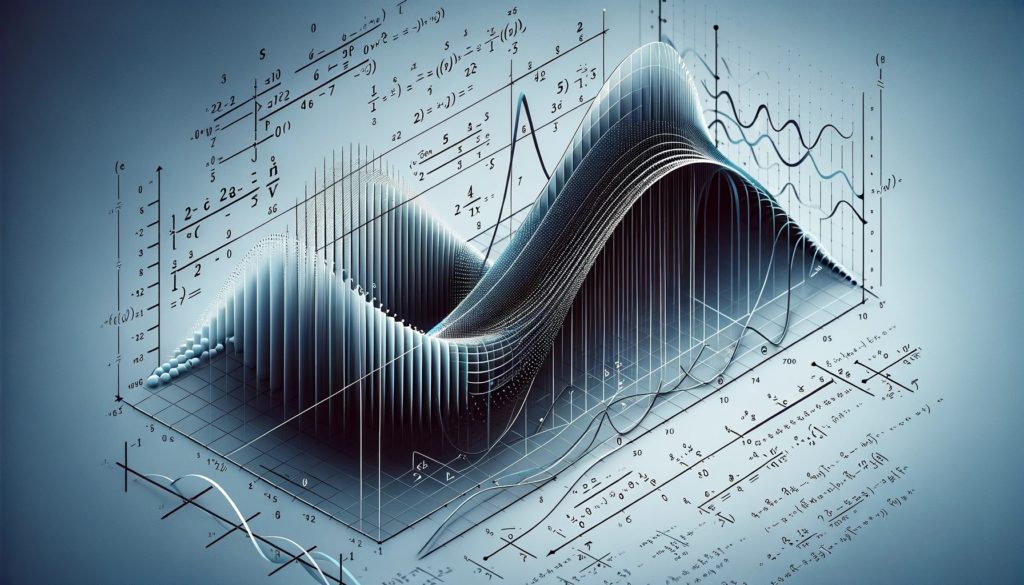
e संख्या वाली अनुक्रम की सीमा… क्या यह सचमुच?
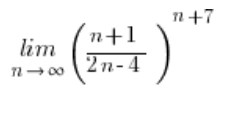
अगर हमने अनुक्रम की सीमाओं के कुछ प्रश्नों को हल कर लिया है, तो हम एक रूटीन में पड़ सकते हैं। और हम इसे e संख्या वाली सीमाओं की तरह गिनने लगते हैं: अंश के अंश में 4 घटाना और जोड़ना, इसे दो अंशों में विभाजित करना, आदि। लेकिन ऐसा करने से हम एक छोटी समस्या का सामना करते हैं…
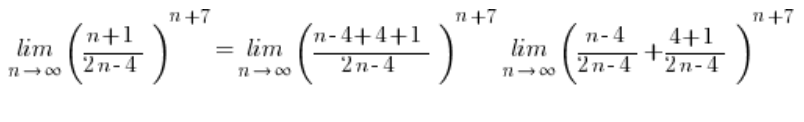
इस बार पहला अंश बिल्कुल भी सरल नहीं होता और न ही एक देता है!
शिक्षक अक्सर इस पर ध्यान नहीं देते, लेकिन हम e संख्या वाली सीमाओं का उपयोग तभी करते हैं जब एक अनिर्धारित रूप 
होता है, और हमारे उदाहरण में:
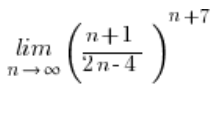
दूसरा भाग:
बहुपदों का भागफल जिसे घात तक बढ़ाया गया है, बिल्कुल 1 की ओर नहीं बढ़ता, बल्कि 
की ओर बढ़ता है, जैसा कि हम इसमें सबसे बड़ी घातों को कोष्ठकों से बाहर निकालकर देख सकते हैं:
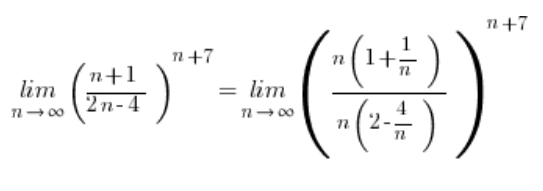
इसलिए हमारे पास 
की स्थिति है, और यह अनुक्रम सीमा उचित सूत्र के अनुसार 0 के बराबर है:
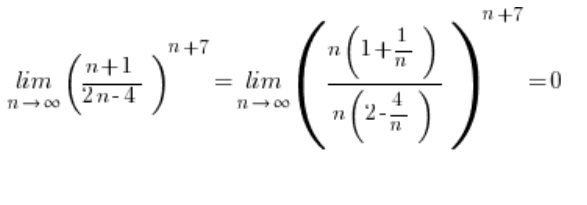
इस प्रकार की सीमाओं की समस्या
इसलिए e संख्या वाली सीमाओं के सूत्रों से अनुक्रम की सीमा का समाधान करने से पहले, यह विचार करने योग्य है कि क्या घात तक बढ़ाया गया व्यंजक बिल्कुल 1 की ओर बढ़ रहा है। बहुपद को बहुपद से विभाजित करने के मामले में, यह जांचना आसान है, बिना कोई गणना किए। यह विभाजन 1 की ओर बढ़ता है, यदि बहुपदों की सबसे बड़ी घातें समान होती हैं और उनके सामने के गुणांक भी समान होते हैं। उस स्थिति में आप e संख्या वाली सीमा की विधि का उपयोग कर सकते हैं। यदि नहीं, तो आपको सबसे बड़ी घात को कोष्ठकों के बाहर निकालना पड़ सकता है।
स्वयं निर्णय लें, एक नज़र में
अंत में, एक अभ्यास। नीचे दी गई सीमाओं को देखें और “एक नज़र” में निर्णय लें कि इनमें से कौन-सा e संख्या की विधि से हल किया जाना चाहिए और कौन-सा सबसे बड़ी घात को बाहर निकालने की विधि से:
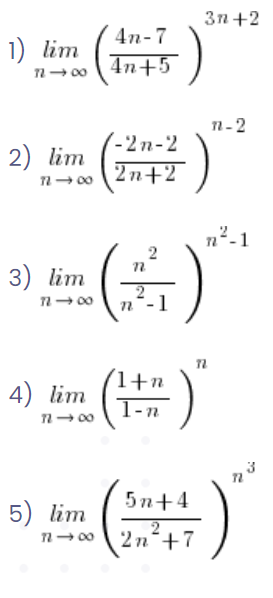
…और ये सभी इतने समान दिखते हैं… 🙂
