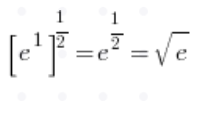e संख्या के सूत्र के साथ एक असामान्य अनुक्रम सीमा

---

संख्या e के सूत्र के साथ सामान्य अनुक्रम सीमा

परंपरागत समस्याएं संख्या e के सूत्र के साथ अनुक्रम सीमा पर काफी “स्वाभाविक रूप से” सूत्र की ओर ले जाती हैं (मैं अपने कोर्स में इसे कैसे करना है, दिखाता हूं):

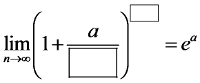लेकिन अगर हमारे पास उस सुंदर भिन्न की बजाय कुछ ऐसा हो जो कोष्ठक में हो:

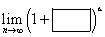अगर कोष्ठक में आयत शून्य की ओर बढ़ता है, और घातांक में त्रिभुज अनंतता की ओर बढ़ता है, तो हमारे पास वास्तव में एक अनिश्चित प्रतीक है – बिल्कुल वही, जिसमें हम संख्या ‘e’ के साथ सूत्र का उपयोग करते हैं। अब क्या करें?

खैर, याद रखें कि किसी भी अभिव्यक्ति को इसके व्युत्क्रम से विभाजन के रूप में प्रस्तुत किया जा सकता है 🙂

उदाहरण के लिए, साधारण, विनम्र संख्या 2 को इस प्रकार लिखा जा सकता है:

तो, यदि वास्तव में आवश्यकता हो तो किसी भी अभिव्यक्ति को “जबरदस्ती” भिन्न बनाया जा सकता है।

संख्या e के सूत्र के साथ एक असामान्य सीमा का उदाहरण

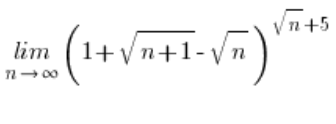
सबसे पहले, यह दिखाना चाहिए कि अभिव्यक्ति शून्य की ओर बढ़ती है। आप इसे सीमा की गणना करके करते हैं:

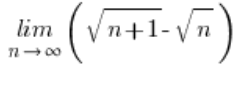– परिणाम वास्तव में शून्य होगा (आप संयुग्म से गुणा करने की विधि का उपयोग कर सकते हैं)।

अब, बदलें:

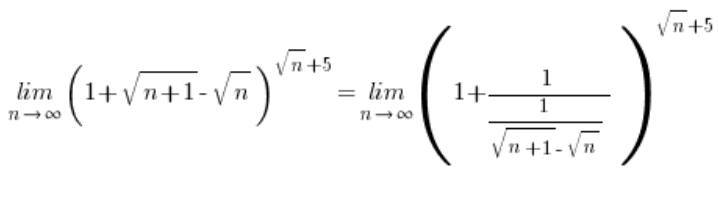
… और ज्ञात योजना के अनुसार जारी रखें:

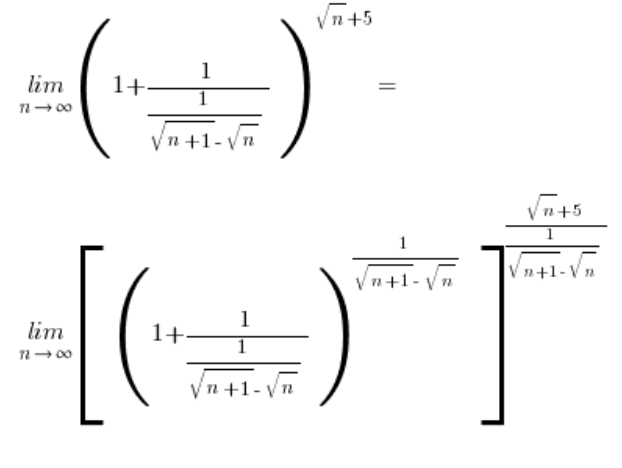
बड़े वर्ग कोष्ठक में सीमा है: 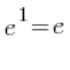– मूलभूत सूत्र के अनुसार, केवल अंतिम चरण शेष है:

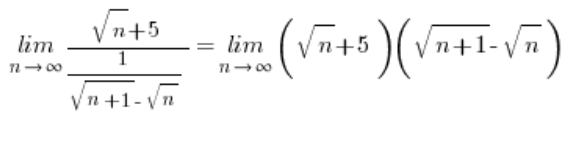
… जो संयुग्म से गुणा करने के बाद समाप्त होता है परिणाम के साथ।

इसलिए, पूरी सीमा बराबर है: