जब जटिल संख्याओं के सवाल हल करते हैं, तो ध्यान रखना चाहिए कि जटिल संख्या त्रिकोणमितीय रूप में इस तरह दिखती है:
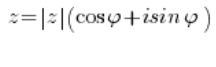
और केवल इस तरह। न ज्यादा, न कम।
इसलिए ध्यान देने की जरूरत है:
जटिल संख्या कब त्रिकोणमितीय रूप में होती है और कब नहीं?
- संख्या:
त्रिकोणमितीय रूप में होती है, जहां संख्या का मापांक 1 के बराबर होता है (), क्योंकि जाहिर है:
- संख्या: त्रिकोणमितीय रूप में नहीं होती है क्योंकि ‘i’ के साथ गुणा किए गए साइन के पहले एक ऋण चिह्न है, जबकि यह एक धन चिह्न होना चाहिए।
इस संख्या को त्रिकोणमितीय रूप में बदलने के लिए, हमें त्रिकोणमितीय सूत्रों का उपयोग करना होगा:
इन सूत्रों का उपयोग करके, हम बदल सकते हैं:
साइन और कोसाइन फलन-आवर्ती होते हैं, इसलिए उनका मान के बराबर होता है। इस विषय पर मैंने और लिखा है: इस पोस्ट में।
तो अंत में हमारे पास है:
…और यह एक त्रिकोणमितीय रूप में संख्या है। - संख्या: त्रिकोणमितीय रूप में नहीं होती है क्योंकि ‘i’ के साथ गुणा किए गए साइन के पहले एक ऋण चिह्न है, जबकि यह एक धन चिह्न होना चाहिए, और कोसाइन के पहले एक ऋण चिह्न है, जबकि यह एक धन चिह्न होना चाहिए।
इस जटिल संख्या को त्रिकोणमितीय रूप में बदलने के लिए, हमें कोष्ठक के सामने के ऋण चिह्न को बाहर निकालना होगा:
संख्या को त्रिकोणमितीय रूप में बदलें (हम पहले से ही जानते हैं…):
तो हमारे पास दो त्रिकोणमितीय रूप में संख्याओं का गुणन है:
त्रिकोणमितीय रूप में संख्याओं को गुणा करने के लिए, हम उनके मापांक को गुणा करते हैं और उनके तर्क को जोड़ते हैं (इसके लिए एक सूत्र है), तो हमारे पास है:
और यह एक त्रिकोणमितीय रूप में संख्या है। - संख्या: त्रिकोणमितीय रूप में नहीं है क्योंकि कोसाइन के पहले एक ऋण चिह्न है, जबकि इसे एक धन चिह्न होना चाहिए।
इस जटिल संख्या को त्रिकोणमितीय रूप में बदलने के लिए, आपको कोष्ठक के सामने ऋण चिह्न निकालना होगा:
संख्या -1 को त्रिकोणमितीय रूप में बदलना होगा (हमने इसे बिंदु 3 में किया), इसी तरह संख्या को त्रिकोणमितीय रूप में बदलना होगा (हमने इसे बिंदु 2 में किया)।
हमें प्राप्त होता है:
त्रिकोणमितीय कार्यों के गुणा के लिए सूत्र का उपयोग करके:
और साइन और कोसाइन कार्यों की आवृत्तता का उपयोग करके:
- संख्या: त्रिकोणमितीय रूप में नहीं है क्योंकि कोसाइन के पहले एक काल्पनिक इकाई ‘i’ है (जो वहाँ नहीं होनी चाहिए), और साइन के पहले कोई काल्पनिक इकाई ‘i’ नहीं है।
आपको हाई स्कूल में सीखी गई त्रिकोणमितीय सूत्रों का उपयोग करना होगा:
हमारे पास है:
और यह त्रिकोणमितीय रूप में एक जटिल संख्या है। - संख्या: त्रिकोणमितीय रूप में नहीं है।
आपको साइन और कोसाइन को बदलना होगा जैसे हमने बिंदु 5 में किया था, और फिर इसे बिंदु 4 की तरह हल करना होगा। - संख्या: त्रिकोणमितीय रूप में नहीं है।
आपको साइन और कोसाइन को बदलना होगा जैसे हमने बिंदु 5 में किया था, और फिर इसे बिंदु 2 की तरह हल करना होगा। - संख्या: त्रिकोणमितीय रूप में नहीं है।
आपको साइन और कोसाइन को बदलना होगा जैसे हमने बिंदु 5 में किया था, और फिर इसे बिंदु 3 की तरह हल करना होगा।
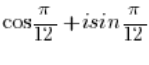त्रिकोणमितीय रूप में होती है, जहां संख्या का मापांक 1 के बराबर होता है (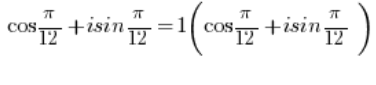
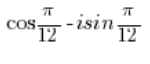), क्योंकि जाहिर है:
त्रिकोणमितीय रूप में नहीं होती है क्योंकि ‘i’ के साथ गुणा किए गए साइन के पहले एक ऋण चिह्न है, जबकि यह एक धन चिह्न होना चाहिए।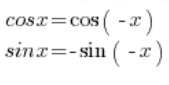
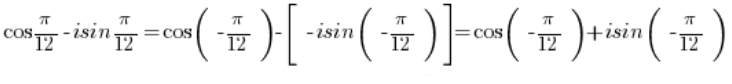
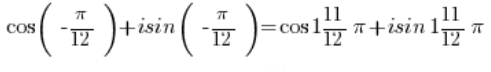
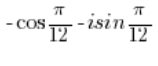-आवर्ती होते हैं, इसलिए उनका मान 
त्रिकोणमितीय रूप में नहीं होती है क्योंकि ‘i’ के साथ गुणा किए गए साइन के पहले एक ऋण चिह्न है, जबकि यह एक धन चिह्न होना चाहिए, और कोसाइन के पहले एक ऋण चिह्न है, जबकि यह एक धन चिह्न होना चाहिए।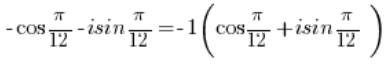
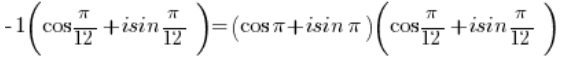
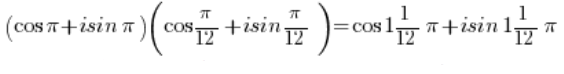
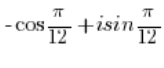को त्रिकोणमितीय रूप में बदलें (हम पहले से ही जानते हैं…):
त्रिकोणमितीय रूप में नहीं है क्योंकि कोसाइन के पहले एक ऋण चिह्न है, जबकि इसे एक धन चिह्न होना चाहिए।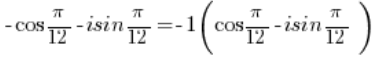
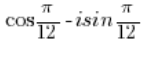को त्रिकोणमितीय रूप में बदलना होगा (हमने इसे बिंदु 2 में किया)।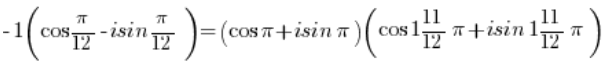
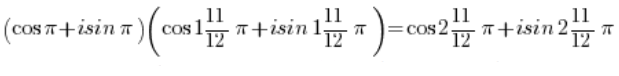
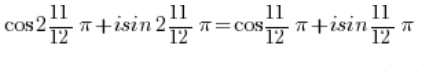
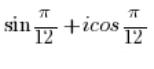त्रिकोणमितीय रूप में नहीं है क्योंकि कोसाइन के पहले एक काल्पनिक इकाई ‘i’ है (जो वहाँ नहीं होनी चाहिए), और साइन के पहले कोई काल्पनिक इकाई ‘i’ नहीं है।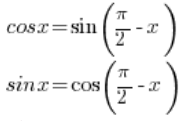
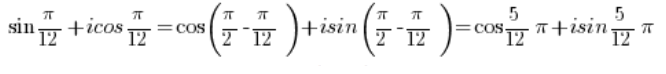
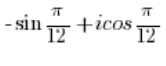त्रिकोणमितीय रूप में नहीं है।
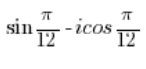त्रिकोणमितीय रूप में नहीं है।
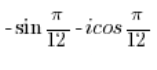त्रिकोणमितीय रूप में नहीं है।शुभकामनाएं! 🙂
