No products in the cart.
Krystian Karczyński- 18 जून 2024
- Komentarz 0
कई लघुगणक वाले अनुक्रमों की सीमाओं के लिए, आप आत्मविश्वास से हाई स्कूल में सीखे गए लघुगणक परिवर्तनों और सूत्रों का उपयोग कर सकते हैं। उदाहरण के लिए:
लघुगणकों वाले अनुक्रम की सीमा का उदाहरण
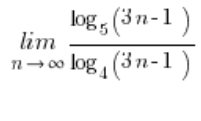
ऐसी स्थितियों में जहाँ लघुगणकों के अलग-अलग आधार होते थे और इसके बारे में कुछ भी नहीं किया जा सकता था, उन्हें सूत्र का उपयोग करके एक आधार में बदल दिया जाता था: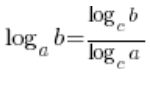 
। हमारी सीमा में, इस आधार को लेना अच्छा और सुविधाजनक होगा: 
। इस प्रकार हमारे पास अनुक्रम की सीमा होगी:
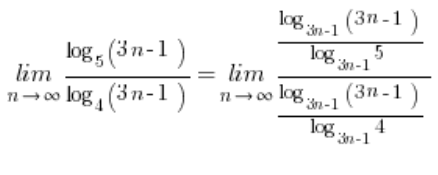
हमें पता है कि 
, जो हमारे अभिव्यक्ति में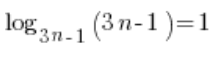 
है। इसलिए:
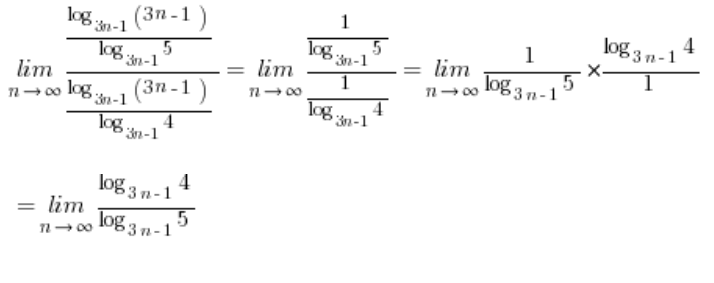
और यह अभिव्यक्ति, हाई स्कूल सूत्र का उपयोग करते हुए फिर से (लेकिन इस बार विपरीत दिशा में), बराबर होगी: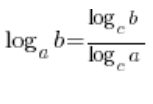 
…
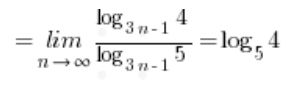
जो स्वाभाविक रूप से परिणाम है (एक अवास्तविक संख्या)।
कोई सीमा विधियों का उपयोग करने की आवश्यकता नहीं थी – हाई स्कूल के लघुगणक परिवर्तन पर्याप्त थे।
क्या आप सीमा की गणना के बारे में और जानना चाहते हैं? मैं अपने कोर्स की सिफारिश करता हूँ 🙂
