यूएलर प्रतिस्थापन के प्रकार I, II, III – अधिक की आवश्यकता नहीं
पिछली पोस्टों में, मैंने दिखाया कि यूएलर प्रतिस्थापन का उपयोग कैसे किया जाता है, निम्न प्रकार की इंटीग्रल्स में:

- यूएलर प्रतिस्थापन के प्रकार I (जब a>0)
- यूएलर प्रतिस्थापन के प्रकार II (जब c>0)
इस पोस्ट में, हम यूएलर प्रतिस्थापन के तीसरे और अंतिम प्रकार से निपटेंगे, जिसका उपयोग हम तब कर सकते हैं, जब इंटीग्रल में:

द्विघात बहुपद ![]() , के दो अलग-अलग मूल हों
, के दो अलग-अलग मूल हों ![]() , यानी जब इसका
, यानी जब इसका  , यानी जब इसे गुणन रूप में लिखा जा सकता है:
, यानी जब इसे गुणन रूप में लिखा जा सकता है: ![]() .
.
लेकिन इससे पहले कि हम आगे बढ़ें, आइए ध्यान दें कि ये तीन मामले:
- पहला प्रकार, जब a>0
- दूसरा प्रकार, जब c>0
- तीसरा प्रकार जब दो अलग-अलग मूल होते हैं
हमें प्रत्येक प्रकार की इंटीग्रल को हल करने की अनुमति देते हैं:

वास्तव में, केवल पहले और तीसरे प्रकार ही पर्याप्त हैं।
क्यों?
मामला, जब ![]() हम इसे अनदेखा कर सकते हैं, क्योंकि द्विघात बहुपद
हम इसे अनदेखा कर सकते हैं, क्योंकि द्विघात बहुपद ![]() बस रेखीय रूप में बदल जाता है
बस रेखीय रूप में बदल जाता है ![]() , जिसे हम यूएलर की तुलना में सरल प्रतिस्थापनों का उपयोग करके हल कर सकते हैं।
, जिसे हम यूएलर की तुलना में सरल प्रतिस्थापनों का उपयोग करके हल कर सकते हैं।
लेकिन जब a<0 (पहले प्रकार के अनुकूल नहीं है) और द्विघात बहुपद के एक या कोई भी मूल नहीं है (तीसरे प्रकार के अनुकूल नहीं है) तो क्या करें?
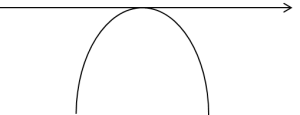
फिर इसका ग्राफ ऐसा दिखेगा (मिडिल स्कूल से याद रखें – बाहें नीचे):
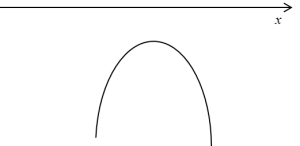
या, यदि इसमें कोई मूल नहीं होते, तो ऐसा:
इसका क्या निष्कर्ष है? कि दोनों ही मामलों में द्विघात बहुपद नकारात्मक मान लेगा (अधिकतम एक बिंदु को छोड़कर), और मैं आपको याद दिला दूं, हम इंटीग्रल की गणना कर रहे हैं:

अर्थात, इंटीग्रल के तहत द्विघात बहुपद जड़ के नीचे है, और जड़ को नकारात्मक मानों से नहीं निकाला जा सकता (हम स्पष्ट रूप से वास्तविक संख्याओं से खेल रहे हैं)। अर्थात, ऐसी फ़ंक्शन का डोमेन अधिकतम एक बिंदु होगा, जो बिल्कुल भी समझ में नहीं आता है, और हम निश्चित रूप से ऐसा उदाहरण नहीं पाएंगे। जब तक कि प्रोफेसर वास्तव में प्रश्नों को बनाने में बहुत थके हुए न हों।
इसलिए, जब a<0 और द्विघात बहुपद ![]() के दो मूल नहीं होते, तो इसे अनदेखा किया जा सकता है, और अब स्पष्ट रूप से देखा जा सकता है कि यूएलर प्रतिस्थापन के पहले और तीसरे प्रकार प्रत्येक प्रकार की इंटीग्रल में फिट बैठते हैं:
के दो मूल नहीं होते, तो इसे अनदेखा किया जा सकता है, और अब स्पष्ट रूप से देखा जा सकता है कि यूएलर प्रतिस्थापन के पहले और तीसरे प्रकार प्रत्येक प्रकार की इंटीग्रल में फिट बैठते हैं:

तो, चलिए यूएलर प्रतिस्थापन के तीसरे प्रकार पर चलते हैं।
यूएलर प्रतिस्थापन के प्रकार III
हमारे पास एक इंटीग्रल है:
 ,
,
जिसमें ![]() का
का  , यानी इसे लिखा जा सकता है:
, यानी इसे लिखा जा सकता है:
![]() ,
,
जहां ![]() इसके मूल हैं।
इसके मूल हैं।
यहां हम जो प्रतिस्थापन करते हैं, वह है:
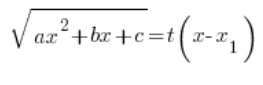
हम इस प्रतिस्थापन को वर्ग करते हैं, बाएँ तरफ का द्विघात बहुपद गुणन रूप में लिखते हैं (हम जानते हैं कि हम कर सकते हैं), दोनों तरफ को ![]() से विभाजित करते हैं, और पिछली प्रतिस्थापनों की तरह क्रमशः निर्धारित करते हैं:
से विभाजित करते हैं, और पिछली प्रतिस्थापनों की तरह क्रमशः निर्धारित करते हैं:
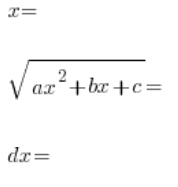
अंत में, हम सभी को प्रारंभिक इंटीग्रल में डालते हैं और एक सामान्यतः कष्टप्रद परिमेय इंटीग्रल पर समाप्त होते हैं।
चलो शुरू करें।
उदाहरण
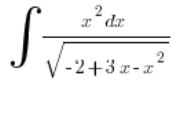
हमारे ![]() (यानि a<0, यानि हम पहले प्रकार के प्रतिस्थापन का उपयोग नहीं करेंगे), हमारे
(यानि a<0, यानि हम पहले प्रकार के प्रतिस्थापन का उपयोग नहीं करेंगे), हमारे ![]() (यानि c<0, यानि हम दूसरे प्रकार के प्रतिस्थापन का उपयोग नहीं करेंगे), लेकिन हमारे
(यानि c<0, यानि हम दूसरे प्रकार के प्रतिस्थापन का उपयोग नहीं करेंगे), लेकिन हमारे ![]() , यानि हम तीसरे प्रकार के प्रतिस्थापन का उपयोग कर सकते हैं।
, यानि हम तीसरे प्रकार के प्रतिस्थापन का उपयोग कर सकते हैं।
पहले हम गणना करते हैं ![]() :
:
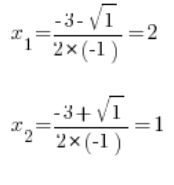
हम यूएलर प्रतिस्थापन के तीसरे प्रकार का उपयोग करते हैं:
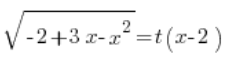
हम दोनों तरफ को वर्ग करते हैं:
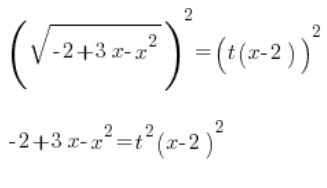
हम बाएँ तरफ के द्विघात बहुपद को गुणन रूप में लिखते हैं (याद रखें ![]() यहां!!!):
यहां!!!):
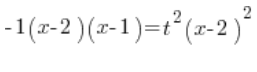
हम दोनों तरफ को ![]() से विभाजित करते हैं:
से विभाजित करते हैं:
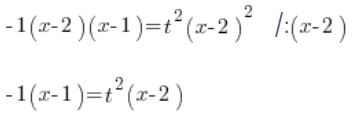
हम ![]() निर्धारित करते हैं:
निर्धारित करते हैं:
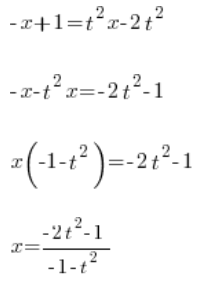
हमारे पास ![]() चर का उपयोग करके निर्धारित होता है
चर का उपयोग करके निर्धारित होता है ![]() । अब हम
। अब हम 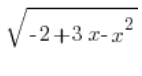 निर्धारित करते हैं।
निर्धारित करते हैं।
हमारे पहले प्रतिस्थापन में लौटते हैं, हमारे पास है:
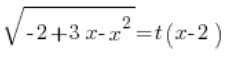
हम निर्धारित 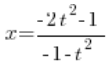 को डालते हैं, और हमारे पास है:
को डालते हैं, और हमारे पास है:
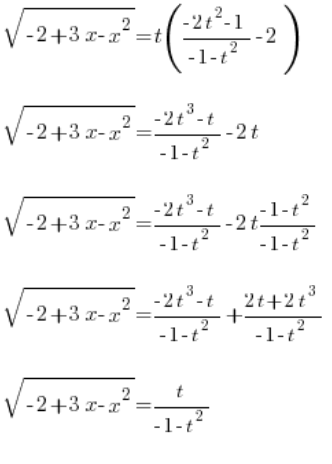
हमने 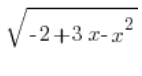 को खूबसूरती से निर्धारित किया है। अब केवल
को खूबसूरती से निर्धारित किया है। अब केवल ![]() बचा है, जिसे हम
बचा है, जिसे हम ![]() का अवकल निकालकर गणना करेंगे:
का अवकल निकालकर गणना करेंगे:
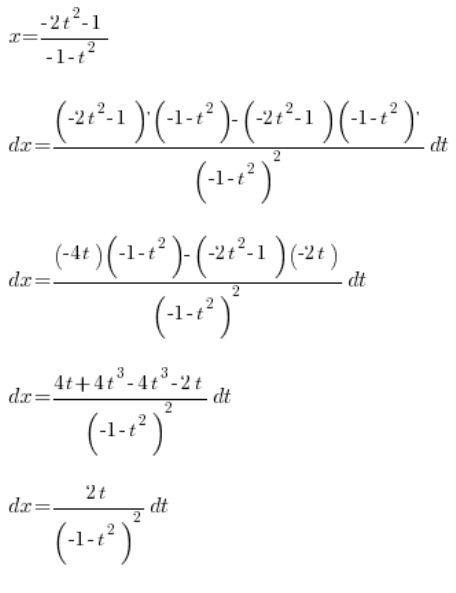
तो हमने निर्धारित किया है:
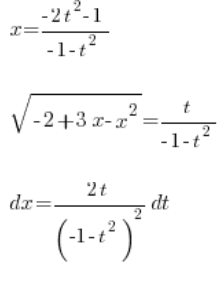
, सब कुछ चर ![]() का उपयोग करके। हम इसे इंटीग्रल में डालते हैं:
का उपयोग करके। हम इसे इंटीग्रल में डालते हैं:
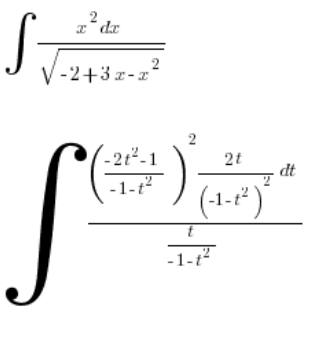
हम सरल बनाते हैं:
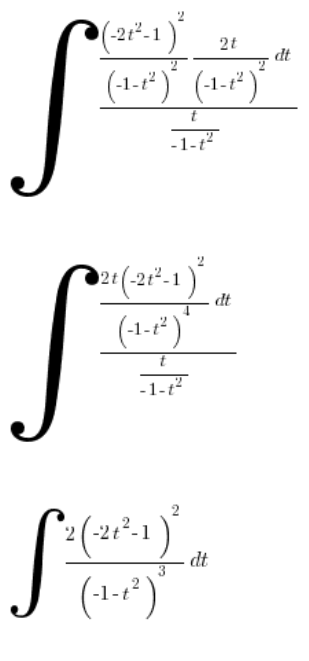
जैसा कि अपेक्षित था, हम वास्तव में जटिल परिमेय इंटीग्रल पर आते हैं, जिसे मैं गणना नहीं करूंगा।
अंत में, यह उल्लेखनीय है कि…
यूएलर प्रतिस्थापन के बारे में नोट
हमारे पास एक इंटीग्रल है:
 ,
,
जिसमें:
- पहला प्रकार, जब a>0
- दूसरा प्रकार, जब c>0
- तीसरा प्रकार जब दो अलग-अलग मूल होते हैं
यह स्पष्ट है कि इसे अक्सर यूएलर के दो प्रतिस्थापनों में से किसी एक का उपयोग करके, या यहां तक कि उनमें से किसी एक का उपयोग करके हल किया जा सकता है (जब a>0, c>0 और साथ ही साथ  )।
)।
कोई समस्या नहीं, हालांकि गणना की आसानी के कारण मैं पहले प्रकार का उपयोग करने की सिफारिश करूंगा, यदि यह काम नहीं करता है, तो दूसरा, और यदि यह भी काम नहीं करता है, तो अंततः तीसरा।
यूएलर प्रतिस्थापन का उपयोग करने के बारे में बस इतना ही, मुझे आशा है कि यह आपके अध्ययन में सहायक होगा, और हमेशा की तरह, पोस्ट के नीचे टिप्पणियों में स्वतंत्र महसूस करें।