No products in the cart.
Krystian Karczyński- 3 जुलाई 2024
- Komentarz 0
मुझे अनिश्चित समाकलन के कोर्स में परिचय किए गए द्विघात फलन के मानक रूप के बारे में बहुत से प्रश्न मिलते हैं।
सूत्र:
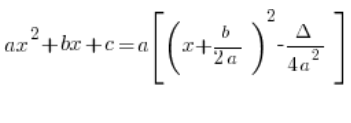
कोर्स के पांचवें पाठ में परिमेय समाकलनों को हल करने की योजना में प्रकट होता है:
यहां a^2 क्यों है?
समस्या यह है कि पहली नज़र में, यह हाई स्कूल में ज्ञात मानक रूप से अलग दिखता है:
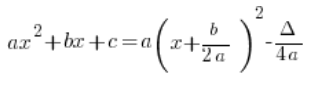
यहां सामान्य प्रश्न है: “आपके सूत्र में 
हर जगह क्यों है?”
सूत्र का परिवर्तन
केवल यह देखना पर्याप्त है कि यदि सूत्र में:
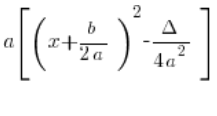
हम 
को वर्ग कोष्ठक के साथ गुणा करते हैं, तो हमें बिल्कुल वही सूत्र मिलता है:
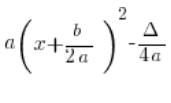
(गुणा करने के बाद तत्व 
के साथ, यह कट जाएगा और हमें 
मिल जाएगा)
इसलिए, दोनों रूप समकक्ष हैं, यानी बस:
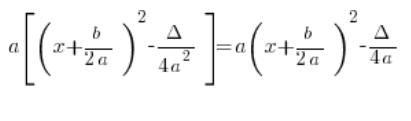
तो फिर इस सूत्र को वर्ग कोष्ठक के साथ और a को कोष्ठक के बाहर क्यों प्रस्तुत करें? क्योंकि परिमेय समाकलनों में ऐसा करना अधिक सुविधाजनक होता है 🙂
समाकलन की गणना के अगले चरणों में, आपको को समाकल चिह्न के सामने (और पहले हर कोष्ठक के आगे) निकालना होगा, तो फिर प्रतीक्षा क्यों करें? 🙂
