कुछ चीजें जो आपको हाई स्कूल में अच्छी तरह से सीखनी चाहिए, लेकिन किसी ने आपको नहीं बताया – भाग 3: द्विघात फलन

यह पोस्ट पहले की दो पोस्टों के बाद तीसरी पोस्ट है, जिसमें मैं आपको उन चीज़ों पर ध्यान देने के लिए कहूंगा जिन्हें कॉलेज में गणित पढ़ाई की शुरुआत में दोहराना महत्वपूर्ण है। इनका तेज़ी से दोहराना आपके कॉलेज जीवन को बहुत आसान बना देगा। पिछली पोस्टों में मैंने निम्नलिखित विषयों पर चर्चा की:

समीकरण की ज्यामितीय व्याख्या

मात्रक

आज की बारी है द्विघात फलन।

द्विघात फलन? लेकिन हमने इसे दो महीने तक किया…

द्विघात फलन का विषय बहुत व्यापक है और मेरा मतलब यह नहीं है कि आप उच्च विद्यालय की पाठ्यपुस्तक लेकर पूरा अध्याय पढ़ें।

आइए हम केवल कुछ महत्वपूर्ण विवरणों, बारीकियों और जालों पर ध्यान दें।

द्विघात फलन बनाम द्विघात समीकरण

द्विघात फलन निश्चित रूप से कुछ इस प्रकार है:

या: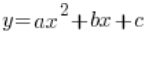

जहां कोई भी संख्या हो सकती है। द्विघात फलनों के उदाहरण हैं:

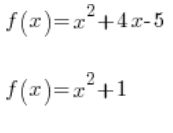
आदि…

द्विघात फलन की अवधारणा को द्विघात समीकरण की अवधारणा से अलग किया जाना चाहिए, उदाहरण के लिए:

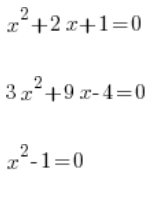
आदि…

यह समान नहीं है!!!!

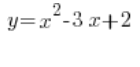एक द्विघात फलन है, जबकि 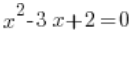एक द्विघात समीकरण है।

यह अंतर न कर पाने के कारण अक्सर कॉलेज में…

भयंकर गलती नंबर 1

उदाहरण के लिए, जब अवकलजों की गणना करते हैं और एक फलन दिया जाता है:

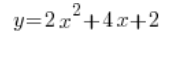
लोग अक्सर ऐसा कुछ करते हैं:

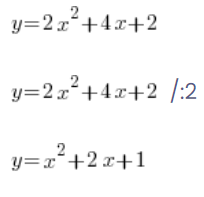
…और आवश्यकतानुसार आगे की गणना करते हैं।

वे यह गलती करते हैं क्योंकि उन्हें याद आता है कि वे समीकरणों में ऐसा कर सकते थे:

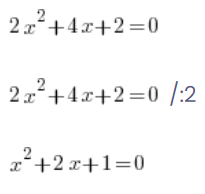
…और समीकरणों में सब कुछ ठीक होता है, आप दोनों पक्षों को विभाजित कर सकते हैं, दाईं ओर का 0 को 2 से विभाजित करने पर वास्तव में 0 होता है और समीकरण समतुल्य (एक ही समाधान होते हैं) होते हैं।

लेकिन आप इसे फलनों के साथ नहीं कर सकते – आपको बाईं ओर y को भी विभाजित करना होगा आदि। फलन के मान को 2 से विभाजित करने पर आपको एक अलग फलन मिलेगा!

आपको फलनों से क्या दोहराना चाहिए?

ज्यादा कुछ नहीं। वास्तव में केवल दो प्रकार के फलन: मानक और गुणक रूप।

द्विघात फलन का मानक रूप

मुझे लगता है कि हमारे पास पहले से ही द्विघात फलन का सामान्य रूप है:

इसका मानक रूप है:

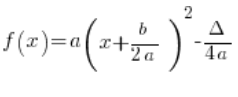
यानी:

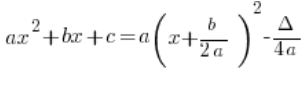
a, b और क्या हैं, यह सभी को पता है, बहुत कम लोग इस पर समस्या रखते हैं कि ।

आप देख सकते हैं कि यदि हम मानक रूप में को बाहर निकालते हैं, तो हमें मिलेगा:

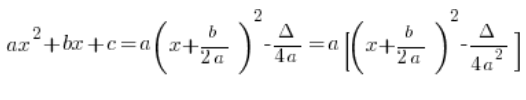
…जो कभी-कभी उपयोगी हो सकता है और कभी-कभी नहीं।

यदि आपने इसे शिखर के निर्देशांक (आमतौर पर और ) की गणना करके और सूत्र में डालकर सीखा है:

तो यह थोड़ा घुमावदार है, लेकिन यह भी अच्छा है।

मानक रूप के सूत्र की शुरुआत में को याद रखें!

द्विघात फलन का गुणक रूप (इसका कारक में विभाजन):

अब हमारे सामान्य द्विघात फलन पर वापस आते हैं:

अक्सर इसे “कारकों में विभाजित” करना होगा, द्विघात फलन के गुणक रूप का उपयोग करके:

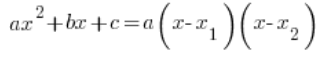
जहां और ज्ञात और पसंद किए गए सूत्रों से गणना की जाती है:

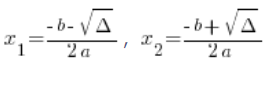
यहां भी आपको को सूत्र के शुरुआत में याद रखना होगा!!!

ध्यान दें कि ये और हमेशा मौजूद नहीं होते हैं (यदि डेल्टा नकारात्मक है, तो वे मौजूद नहीं होते हैं), जिसका मतलब है कि फलन को हमेशा गुणक रूप में नहीं लिखा जा सकता है, यानी द्विघात फलन को हमेशा कारकों में विभाजित नहीं किया जा सकता है।

द्विघात समीकरणों से आपको क्या दोहराना चाहिए?

द्विघात समीकरणों के साथ, मुझे लगता है कि चीजें बहुत बुरी नहीं हैं। हम आमतौर पर सामान्य समीकरण को हल कर लेते हैं:

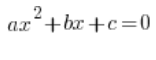
उदाहरण के लिए:

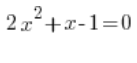
हम बस गणना करते हैं:

फिर, यदि डेल्टा गैर-नकारात्मक है, तो समीकरण का समाधान:

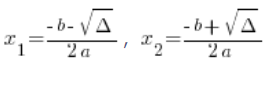
याद रखें कि वहां हर जगह है और केवल 2 नहीं है!

हालांकि, मैं समीकरण के विशेष मामले पर ध्यान देना चाहूंगा:

यहां कई गलतियां होती हैं। उदाहरण के लिए:

भयंकर गलती नंबर 2

वास्तव में गलती क्या है? संख्या 2 वास्तव में समीकरण का समाधान है, लेकिन इस समीकरण का दूसरा समाधान, अर्थात् संख्या -2 को पूरी तरह से छोड़ दिया गया है। इसे होना चाहिए:

नकारात्मक समाधान केवल ज्यामिति में छोड़ा जा सकता है (क्योंकि दूरी नकारात्मक नहीं हो सकती)।

समीकरण के रूप में एक और समस्या: है:

भयंकर गलती नंबर 3

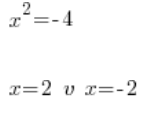
जो निश्चित रूप से बकवास है, क्योंकि 2 वर्ग का मान -4 नहीं होता है। वास्तव में, कोई भी संख्या वर्ग का मान -4 नहीं होता (जिन्होंने पहले से ही सम्मिश्र संख्या पढ़ी है, वे चुप रहें)। समीकरण:

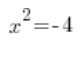
…का कोई समाधान नहीं है।

इसलिए सतर्क रहें। समीकरण के दो समाधान हैं, और समीकरण का कोई समाधान नहीं है।

मैं आपको अब तक कही गई सभी बातों को शांति से दोहराने के लिए आमंत्रित करता हूं और टिप्पणी में सवाल पूछने के लिए।