असंततियों के दो प्रकार (कार्य सीमा)

---

बिंदु पर किसी फलन की सततता

जैसा कि हम सभी जानते हैं (कम से कम मेरी सीमाओं के पाठ्यक्रम से), फलन बिंदु पर सतत है, जब:

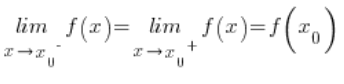
यानी जब इस बिंदु पर इस फलन की बाईं ओर की सीमा इस बिंदु पर फलन की दाईं ओर की सीमा के बराबर होती है जो इस बिंदु पर फलन के मान के बराबर होती है।

यदि इन समानताओं में से कोई भी पूरी नहीं होती है, तो फलन बिंदु परसतत नहीं है, और उस बिंदु को विच्छेदन बिंदु कहा जाता है।

इस नामकरण में, हम एक कदम और आगे बढ़ सकते हैं और विच्छेदन बिंदुओं को अलग कर सकते हैं। हम इसे इस प्रकार करते हैं:

पहली प्रकार के विच्छेदन बिंदु

जब बिंदु को पहली प्रकार का विच्छेदन बिंदु कहा जाता है, अगर सीमाएँ 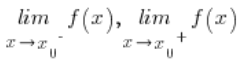सीमित हैं (यानी बस संख्याएँ हैं)।

इसके अलावा, यदि ये सीमाएँ एक-दूसरे के बराबर हैं, तो पहली प्रकार के विच्छेदन बिंदु को हटाने योग्य कहा जाता है।

दूसरी प्रकार के विच्छेदन बिंदु

जब बिंदु को दूसरी प्रकार का विच्छेदन बिंदु कहा जाता है, अगर सीमाओं में से कोई एक 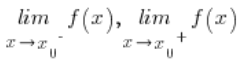सीमित नहीं है (यानी बस धनात्मक या ऋणात्मक अनंत के बराबर है)।

उदाहरण 1

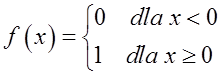
इस फलन में बिंदु पर एक विच्छेदन बिंदु है (क्योंकि इस बिंदु पर बाईं ओर की सीमा 0 है, और दाईं ओर की सीमा 1 है)। यह पहली प्रकार का विच्छेदन बिंदु है क्योंकि इस बिंदु पर बाईं ओर और दाईं ओर की सीमाएँ सीमित हैं (0 और 1)। यह हटाने योग्य पहली प्रकार का विच्छेदन बिंदु नहीं है, क्योंकि सीमाएँ बराबर नहीं हैं।

उदाहरण 2

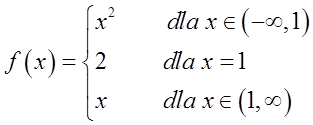
इस फलन में बिंदु पर एक विच्छेदन बिंदु है (क्योंकि इस बिंदु पर बाईं और दाईं सीमाएँ इस बिंदु पर फलन के मान के बराबर नहीं हैं)। यह पहली प्रकार का विच्छेदन बिंदु है क्योंकि बाईं और दाईं सीमाएँ सीमित हैं (और बराबर 1 हैं)। यह हटाने योग्य पहली प्रकार का विच्छेदन बिंदु है क्योंकि बाईं और दाईं सीमाएँ बराबर हैं।

उदाहरण 3

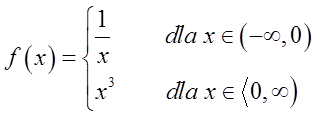
इस फलन में बिंदु पर एक विच्छेदन बिंदु है (क्योंकि इस बिंदु पर बाईं और दाईं सीमाएँ बराबर नहीं हैं)। यह दूसरी प्रकार का विच्छेदन बिंदु है क्योंकि इस बिंदु पर बाईं ओर की सीमा के बराबर है।