Currently Empty: zł0.00
Krystian Karczyński- 16 अप्रैल 2024
- Comment 0
समाकलन के सूत्रों का व्युत्पादन
व्युत्पादन के सूत्र अंतरिक्ष से नहीं आए हैं, वास्तव में ये व्युत्पादन की परिभाषा से निकाले गए हैं:
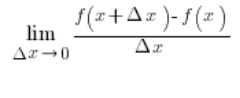
x के वर्गमूल का व्युत्पन्न
चलिए उदाहरण के लिए x के वर्गमूल के व्युत्पन्न का सूत्र निकालते हैं: 
। हमें प्राप्त होना चाहिए: 
(बुनियादी व्युत्पादन के सूत्रों के अनुसार – सूत्र संख्या 5).
हमारे पास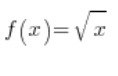 
है। आइए शुरू करें। परिभाषा से समाकलन के सूत्र में प्रतिस्थापन करने पर हमें प्राप्त होगा:
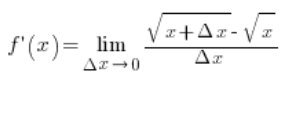
इस प्रकार अंश और हर को मिलाकर गुणा करके…
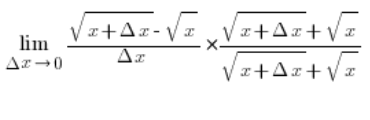
…और अंश में पूर्ण वर्ग सूत्र का उपयोग करते हुए, हम अपरिमेयता को समाप्त कर इस पर आएंगे:
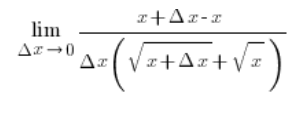
अंश के ऊपरी भाग में x रद्द हो जाएंगे और हम प्राप्त करेंगे…
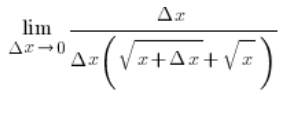
…और अंश और हर में 
के रद्द होने के बाद:
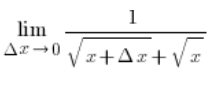
चूंकि 
इसका मतलब है कि:
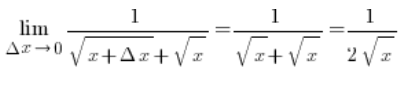
तो हम घर पहुँच गए हैं। समाकलन का सूत्र निकाला गया है।
अधिक उदाहरण
अन्य सूत्रों के साथ प्रयोग करने के लिए स्वतंत्र महसूस करें, मैं आपको प्रोत्साहित करता हूँ!
डेरिवेटिव्स और फंक्शन विश्लेषण कोर्स
विभिन्न मामलों को कदम दर कदम हल किया जा सकता है, जिन्हें आप मेरे डेरिवेटिव्स और फंक्शन विश्लेषण कोर्स में पा सकते हैं।
अधिक सामान्य मामले
डेरिवेटिव के लिए एक सूत्र निकालने का कार्य हमेशा उपयुक्त सीमा की गणना करने के लिए आता है, जहाँ ‘x’ को एक स्थिर माना जाता है। यह आसान या कठिन हो सकता है, लेकिन आप फ़ंक्शन की सीमाएँ की गणना करते समय आपके द्वारा पहले से जानी गई विधियों और तरकीबों का उपयोग कर सकते हैं।
एक आपत्ति के साथ।
दुर्भाग्यवश – लॉपिटल का नियम लागू नहीं होता है। क्यों? इसलिए कि इसमें डेरिवेटिव का उपयोग होता है।
मैं आपको अपने कार्य की याद दिलाता हूँ – आपको परिभाषा से फ़ंक्शन का डेरिवेटिव गणना करनी है, बिना सूत्र के ज्ञान के। और लॉपिटल का नियम अक्सर डेरिवेटिव के सूत्र का उपयोग करता है!
