मध्य विद्यालय में आपको जो कुछ अच्छी तरह से सीखना चाहिए था, लेकिन किसी ने आपको नहीं बताया – भाग 2: मात्राएं

---

मात्राएं – लेकिन वास्तव में यह कभी नहीं था …

ठीक है, मुझे 100% यकीन नहीं है कि नियमित, वार्षिक सामग्री कटौती के बाद मात्राएं अभी भी हाई स्कूल में हैं। मुझे भी जांचने का मन नहीं है, क्योंकि क्यों परेशान होना।

उन्हें विस्तारित प्रोफ़ाइल में होना चाहिए। वास्तव में होना चाहिए।

ठीक है, लेकिन इसे किसे ज़रूरत है?

अधिकांश गणितीय परिभाषाओं और प्रमेयों में, “प्रत्येक” और “अस्तित्व” जैसे अवधारणाओं का उपयोग किया जाता है।

अधिकांशतः कुछ अधिक जटिल अनुक्रमों में, जैसे “दो प्रत्येक संख्याओं के बीच अनंत संख्याएं होती हैं” (यह कुछ हद तक अर्ध-औपचारिक और असटीक है), या: “प्रत्येक गैर-ऋणात्मक वास्तविक संख्या के लिए एक सटीक मूल है”, या: “अस्तित्व कुछ-कुछ, कि प्रत्येक कुछ-कुछ के लिए अस्तित्व एक और कुछ-कुछ” (यह कुछ और की गणितीय परिभाषा है)।

कॉलेज में, आपको इस तरह से दी गई परिभाषाओं और प्रमेयों का एक पूरा ढेर मिलेगा, व्याख्यान के दौरान तेजी से बोला गया और एक ही बार में, या – और भी बदतर – बोर्ड पर सीधे रूप में लिखा गया:

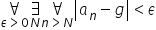
तो यह अच्छा होगा (इसके बजाय कि हाथ उठाओ और प्रोफेसर से पूछो कि क्या इसे “फिर से ड्रॉ” करना है), कि आपने पहले से ही ऐसे सूत्रों को सही ढंग से पढ़ने का तरीका सीखा हो। फिर आप सीधे परिभाषा में “घुसने” के चरणों पर जा सकते हैं, कुछ उदाहरणों पर “कैसे काम करता है” का अवलोकन कर सकते हैं आदि।

सामान्य और विशेष मात्रा – आइए उन्हें बेहतर जानें

“प्रत्येक”, “प्रत्येक के लिए” – यह एक सामान्य मात्रा है, जिसे इस प्रकार दर्शाया जाता है: ।

“अस्तित्व”, “ऐसा अस्तित्व” – यह एक विशेष मात्रा है, जिसे इस प्रकार दर्शाया जाता है: ।

मैं इन विशेष मात्रा प्रतीकों का उपयोग और सिफारिश करता हूं क्योंकि वे निश्चित रूप से मिश्रित नहीं होंगे।

– एक उलटा बड़ा A है (अंग्रेजी “all” से – प्रत्येक)।

– एक उलटा बड़ा E है (अंग्रेजी “exists” से – अस्तित्व)।

मात्राओं के लिए अन्य प्रतीक भी हैं: Λ (“प्रत्येक के लिए”) और V (“अस्तित्व”) – लेकिन मैं उनके साथ काम नहीं करूंगा, क्योंकि वे हर किसी को भ्रमित करते हैं।

मात्राओं का उपयोग करके लिखे गए गणितीय सूत्र

सबसे सरल सूत्र इस प्रकार हैं:

– हम पढ़ते हैं: “प्रत्येक x के लिए” (इसे इस प्रकार भी लिखा जा सकता है: , लेकिन यह फिर से भ्रमित हो जाता है, इसलिए मैं इसे नहीं करूंगा)

– हम पढ़ते हैं: “अस्तित्व x”

हालांकि, सामान्यतः, सूत्र अधिक जटिल होते हैं, उदाहरण के लिए:

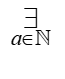– हम पढ़ते हैं: “अस्तित्व a जो प्राकृतिक संख्या है”, या: “अस्तित्व a, जो प्राकृतिक संख्याओं से संबंधित है”, या हिंदी में कोई अन्य अभिव्यक्ति, जो मामले का सार दर्शाती है, अर्थात:

1. अस्तित्व a

2. a एक प्राकृतिक संख्या है

यहाँ कोई “कठोर” भाषाई नियम नहीं हैं कि प्रत्येक शब्द क्या होना चाहिए और यह “अस्तित्व a” होना चाहिए या “ऐसा a का अस्तित्व” होना चाहिए।

सूत्रों को आपस में जोड़ा जा सकता है और आम तौर पर जोड़ा जाना चाहिए, उदाहरण के लिए:

\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,

मतलब:

“प्रत्येक x>4 के लिए, एक n का अस्तित्व है जो प्राकृतिक संख्याओं से संबंधित है”

हम इसका मतलब यह समझते हैं कि प्रत्येक x>4 के लिए “हम” एक n पाएंगे जो प्राकृतिक संख्याओं से संबंधित है, ताकि प्रत्येक ऐसे x के लिए उपयुक्त n चुना जाए। मात्राएँ एक दूसरे के साथ तार्किक रूप से संबंधित हैं, यह दो स्वतंत्र सूत्र नहीं हैं जो एक के बगल में लिखे गए हैं।

अधिक …

क्रम का महत्व है

पिछले सूत्र के समान सूत्र, केवल मात्राओं के क्रम को बदलकर:

\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,

…हम इसे अलग तरह से पढ़ेंगे:

“अस्तित्व a जो एक प्राकृतिक संख्या है, ताकि x जो 4 से बड़ा हो …”

हम समझते हैं कि पहले हमारे पास कुछ n है (जिसके बारे में हम जानते हैं कि इसका अस्तित्व है) और केवल इस विशेष n के लिए कुछ ऐसा होता है कि सभी x>4 के लिए कुछ होता है।

उदाहरण – प्रसंग

यहां का शास्त्रीय उदाहरण है, कार्य अनुक्रम की बिंदु-आधारित और समान अभिसरण की परिभाषा, जो केवल … मात्राओं के क्रम द्वारा भिन्न है (मैंने इन परिभाषाओं को थोड़ा सरल किया है):

बिंदु-आधारित अभिसरण:

समान अभिसरण:

समान अभिसरण की परिभाषा में, जो मात्रा प्रारंभ में बिंदु-आधारित में थी, वह अंत में है। विवरण में जाए बिना, इससे पूरे सूत्र का अर्थ बदल जाता है।

बिंदु-आधारित अभिसरण में, हम पहले (हम बाएं से पढ़ते हैं) कुछ मनमाना x लेते थे, फिर सूत्र को पढ़ते हुए हम इस निष्कर्ष पर पहुंचे कि प्रारंभ में निर्धारित x के लिए अनुक्रम में कार्य मान और “सीमा” कार्य के बीच की दूरी अनंतता में कम हो जाती है।

समान अभिसरण में, हमने पहले निर्धारित किया कि उपयुक्त कार्य मानों के बीच की दूरी अनंतता में कम हो जाती है, और फिर हम इस निष्कर्ष पर पहुंचे कि यह किसी भी x के लिए होता है।

परिभाषाओं, प्रमेयों का लेखन

मात्राओं को पढ़ने की जानकारी होने के कारण, गणितीय परिभाषाओं और प्रमेयों का लेखन हमारे लिए पहले से ही खुला है। उदाहरण के लिए:

\underset{x\in\mathbb{R}}{\mathop{\forall }}\,{{x}^{2}}\ge 0

हम इसे इस प्रकार पढ़ेंगे: “प्रत्येक वास्तविक संख्या x के लिए, x का वर्ग शून्य से बड़ा या बराबर है”, या अधिक सुगम: “प्रत्येक संख्या x का वर्ग गैर-ऋणात्मक है” – मैं निश्चित रूप से परिभाषाओं और प्रमेयों को अधिक रंगीन भाषा में पढ़ने के पक्ष में हूं।

ऊपर का वाक्य सत्य है। हमारे पास गलत वाक्य लिखने में भी कोई समस्या नहीं है:

\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1

जिसे हम पढ़ेंगे: “एक धनात्मक संख्या a का अस्तित्व है, ताकि प्रत्येक संख्या x जो इस a से बड़ी है, a को x से विभाजित करने पर यह 1 से बड़ा होता है”, जो निश्चित रूप से गलत है (क्योंकि बड़ी संख्या से विभाजित धनात्मक संख्या कभी भी 1 से बड़ी नहीं होगी और ऐसी कोई संख्या नहीं है)।

और अब पिछले पोस्ट से अनुक्रम की सीमा की परिभाषा को लेते हुए:

हम इसे इस प्रकार पढ़ेंगे (कुछ स्पष्टीकरण जोड़ते हुए):

“किसी भी जो शून्य से बड़ा है, हम अनुक्रम की एक पद संख्या पाएंगे , ताकि प्रत्येक अनुक्रम पद जो से बड़ी संख्या वाली है, इस अनुक्रम पद और सीमा के बीच की दूरी (मूल्य निरपेक्ष दूरी है) से कम होगी”

हम एक और अधिक मानवतापूर्ण भाषा का उपयोग भी कर सकते हैं:

“चाहे हम प्रारंभ में कितनी भी छोटी दूरी क्यों न निर्धारित करें, हम अनुक्रम की एक पद संख्या पाएंगे, ताकि इस अनुक्रम के सभी बाद के पद सीमा के करीब होंगी जितनी प्रारंभ में निर्धारित की गई दूरी “