Granica ciągu Wykład 2
Temat: Wyznaczanie granicy ciągu z definicji
Streszczenie
W artykule pokażę, jak w praktyce można “wyczuć” definicję granicy ciągu na konkretnych przykładach. Przypomnijmy sobie definicję granicy ciągu:
Definicja granicy ciągu
Liczbę g nazywamy granicą ciągu wtedy i tylko wtedy, gdy:
\underset{\varepsilon >0}{\mathop{\forall }}\,\underset{N}{\mathop{\exists }}\,\underset{n>N}{\mathop{\forall }}\,\left| {{a}_{n}}-g \right|<\varepsilonChodziło o to, że dla dowolnie małego, obranego z góry, epsilona ( \varepsilon ), znajdziemy taki numer wyrazu ciągu ( N ), że wszystkie wyrazy z kolejnymi numerami większymi od N ( n>N ) będą miały odległość od granicy g mniejszą od epsilona ( \left| {{a}_{n}}-g \right|<\varepsilon ) – nieważne, jak mały by ten ustalony epsilon nie był.
Trudne? No jasne, że trudne. Żeby zrozumieć, potrzeba praktyki. Zobaczymy sobie jak to działa na przykładach.
Przykład 1 na obliczanie od którego wyrazu ciągu spełniona jest nierówność dla danego epsilona
Dany jest ciąg o wyrazie ogólnym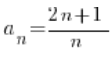 
i granicy 
. Dla epsilona równego 
– które wyrazy ciągu spełniają nierówność 
?
W zadaniu ustaliliśmy epsilon na 0,017. Trzeba obliczyć, od którego wyrazu odległości wyrazów ciągu od granicy będą już mniejsze od tych 0,017. Wyciągnij kalkulator, O.K.?
Najpierw bardzo powoli, namacamy sobie o co chodzi…
Nasz ciąg rozpisany wyraz po wyrazie wyglądał by tak:
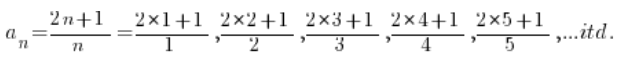
Kolejne wyrazy otrzymuję podstawiając za na konkretne numery. Porządkując będę miał:
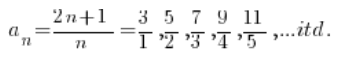
Czyli:
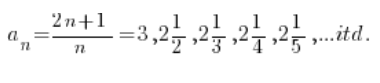
Kolejne wyrazy ciągu będą coraz “bliżej” liczby 2. Nasze zadanie to znaleźć taki numer wyrazu ciągu, od którego odległości od dwójki będą mniejsze od zadanych .
Z pewnością nie będzie to pierwszy wyraz. Jest on równy 3. Jego odległość od granicy (g=2) jest równa 1! To znacznie więcej od żądanego .
Nie będzie to także wyraz drugi ( odległość=
, czyli więcej od ), ani żaden z pierwszych pięciu przeze mnie wypisanych.
Nie będzie to wyraz pięćdziesiąty, bo równy on jest 
, a jego odległość od 2 równa jest 0,02, czyli wciąż więcej od zadanego .
Za to wyraz setny spełnia zadany warunek, bo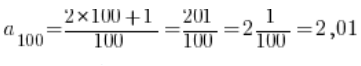 
, jego odległość od dwóch jest równa 0,01, czyli jest mniejsza od 0,017. Są jednak wyrazy o mniejszych od 100 numerach, które warunek ten również spełniają. Naszym zadaniem jest znaleźć numer graniczny, od którego odległość wyrazów ciągu od 2 jest już mniejsza niż 0,017. Skoro odległość wyrazu pięćdziesiątego warunku nie spełnia, a setnego spełnia, wydaje się, że będzie to jakiś wyraz pomiędzy pięćdziesiątym, a setnym… Jak go znaleźć dokładnie?
Przypominamy sobie definicję…
\underset{\varepsilon >0}{\mathop{\forall }}\,\underset{N}{\mathop{\exists }}\,\underset{n>N}{\mathop{\forall }}\,\left| {{a}_{n}}-g \right|<\varepsilonI nierówność z niej…
z tej definicji to ogólny wyraz ciągu, w naszym przykładzie jest równy .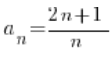 
mamy zadany z góry , a granica g równa jest 2. Wstawiamy to wszystko do nierówności i mamy:
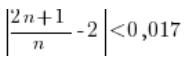
Sprowadzamy w środku wartości bezwzględnej do wspólnego mianownika:
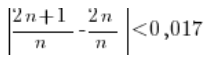
Odejmujemy i mamy:
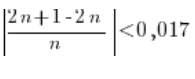
Czyli:
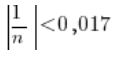
Teraz trochę trudniej. Po lewej strony nierówności w środku wartości bezwzględnej mamy 
. To wyrażenie jest zawsze dodatnie, bo n oznacza numer wyrazu ciągu i bierzemy za niego liczby takie jak: 1, 2, 10. Czyli mamy wartość bezwzględną z liczby dodatniej. Możemy zatem ją opuścić, bo wartość bezwzględna z liczby dodatniej jest zawsze dodatnia:
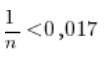
Mnożymy obie strony przez n i znowu musimy się pozastrzegać, że ‘n’ jest zawsze dodatnie i nie zmieni to na pewno znaku nierówności. Otrzymamy po tym przemnożeniu obu stron:
Teraz obie strony dzielimy przez 0,017 (używamy kalkulatora i bierzemy jakieś rozsądne przybliżenie).
Patrząc na tą nierówność i pamiętając, że ‘n’ oznacza numer wyrazu ciągu – jaka będzie odpowiedź?
Odpowiedź
Wszystkie wyrazy ciągu o numerach od 59 w górę spełniają nierówność. W tym ciągu odległość wyrazu 58-go od 2 nie jest jeszcze mniejsza od zadanego epsilona, ale 59-tego, 60-tego, 61-go,… i każdego następnego już tak.
Przykład 2 na obliczanie od którego wyrazu ciągu spełniona jest nierówność dla danego epsilona
Dany jest ciąg o wyrazie ogólnym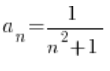 
i granicy 
. Dla epsilona równego 
– które wyrazy ciągu spełniają nierówność ?
Ten przykład jest bardzo podobny do poprzedniego. Epsilon mamy ustalony na 
. Trzeba obliczyć, od którego wyrazu odległości wyrazów ciągu od granicy będą mniejsze od tej wartości.
Rozpiszmy ciąg:
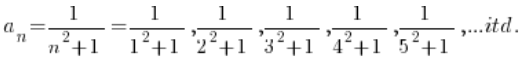
Czyli…
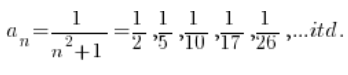
Wyrazy ciągu są coraz mniejsze i mniejsze, zbliżając się do zera. Trzeba wyznaczyć, które mają tą odległość mniejszą od .
Znowu nie będzie tak łatwo, “na oko” widać, że nie będzie to żaden z pierwszych pięciu wyrazów. Przejdźmy może do razu do rzeczy…
Do nierówności z definicji wstawiamy odpowiednie wartości:
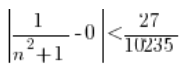
Czyli…
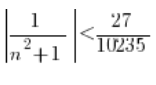
Wartość bezwzględną możemy znowu opuścić, bo 
jest zawsze dodatnie, można więc zapisać:
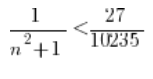
Obie strony możemy pomnożyć przez 
, bo jest zawsze większe od zera…
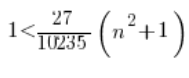
Obie strony mnożymy przez 10235 (żeby było łatwiej) i mamy:
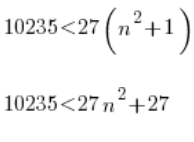
Przenosimy 27 na lewo:
Obie strony dzielimy przez 27 (kalkulator) i w przybliżeniu:
‘n’ może być tylko dodatnie (jak to jednak życie ułatwia, prawda?) więc możemy zapisać:
Czyli w przybliżeniu:
Mamy więc:
Odpowiedź
Wszystkie wyrazy ciągu począwszy od 20-tego spełniają nierówność.
Przykład 1 na obliczanie granicy ciągu z definicji
Zróbmy jeszcze inne zadanie, w którym trzeba będzie “pogrzebać” w definicji granicy ciągu:
Pokaż z definicji, że granicą ciągu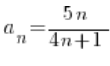 
jest liczba 
.
Korzystając z definicji, należy pokazać, że dla dowolnie małego istniał taki numer wyrazu ciągu, od którego już kolejne wyrazy będą spełniać nierówność:
A w naszym konkretnym przykładzie, trzeba pokazać, że dla dowolnie małego epsilona dla wszystkich n począwszy od jakiegoś spełniona będzie nierówność:
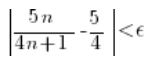
Zrobimy to wyznaczając ‘n’ z powyższej nierówności. Na początku sprowadzamy do wspólnego mianownika…
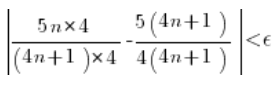
Po lekkich porządkach:
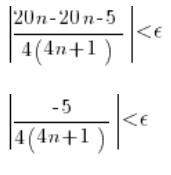
Tą wartość bezwzględną po lewej możemy rozbić – na przykład – tak:
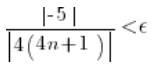
Czyli:
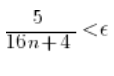
Obie strony możemy pomnożyć przez 
(bo jest to zawsze dodatnie).
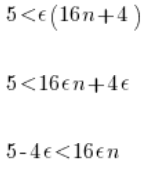
Obie strony dzielimy przez 
(możemy, bo w definicji granicy jest zawsze dodatni):
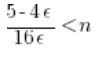
I teraz: n to numery wyrazów ciągu. Są coraz większe i większe. Jakikolwiek ustalimy sobie po lewej stronie nierówności, otrzymamy tam jakąś stałą liczbę. Choćby była ona bardzo wielka jednak – i tak, skoro n rośnie i rośnie, to w końcu prawa strona nierówności “przeskoczy” lewą i od jakiegoś n nierówność będzie spełniona, niezależnie od wyboru .
Pokazaliśmy więc z definicji, co mieliśmy pokazać.
Zróbmy jeszcze na koniec przykład w drugą stronę…
Przykład 2 na obliczanie granicy ciągu z definicji
Sprawdź z definicji, czy granicą ciągu 
, gdzie 
jest większe od 1, jest liczba 
.
Zwróćmy uwagę na niuansik. W poprzednim przykładzie w treści zadania było “Wykaż, że…” – czyli wiadomo było z góry, że tamta liczba była granicą ciągu i trzeba było to tylko udowodnić. Tutaj mamy “Sprawdź, czy…” – a więc być może nasza liczba granicą ciągu nie będzie w ogóle.
Zaczynamy od nierówności z definicji…
Do której podstawiamy odpowiednie wartości…
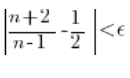
Znowu próbujemy wyznaczyć ‘n’ z powyższej nierówności.
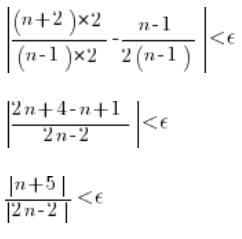
Wartości bezwzględne można opuścić, bo – zwróć uwagę na treść zadania – powiedziane jest, że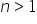 
, czyli wartość bezwzględna na dole jest liczona z liczby dodatniej.
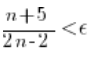
Obie strony mnożymy przez mianownik (można z tych samych powodów, dla których opuściliśmy wartość bezwzględną):
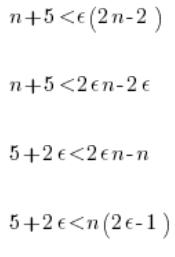
Przez 
podzielić tak sobie nie możemy, bo dla pewnych wartości wyrażenie jest dodatnie, a dla pewnych wyrażenie jest ujemne. Jeżeli ustalilibyśmy na przykład bardzo malutkie (możemy, bo ono mogło być dowolne) wyrażenie będzie ujemne i po podzieleniu obu stron przez: (pamiętamy o zmianie znaku nierówności po przemnożeniu obustronnym przez ujemną wartość!):
Mamy więc (ze względu na odwrócony znak nierówności) sytuację zupełnie odwrotną, niż w poprzednim przykładzie. Po lewej jakąś ustaloną liczbę. Po prawej liczby coraz większe i większe. Można stwierdzić, że od pewnych n-ów nierówność NIE będzie spełniona (a miała być spełniona dla dowolnego epsilon).
Zatem liczba z zadania nie jest granicą ciągu.
Kliknij, aby przypomnieć sobie definicję granicy ciągu (poprzedni Wykład) <–
Kliknij, dowiedzieć się więcej o wyrażeniach nieoznaczonych w granicach ciągu (następny Wykład) –>
Witam, jak poradzic sobie z przykładem, w którym trzeba wykazac z definicji ze granicą ciągu jest nieskonczonosc? tak samo mamy ją “odjąc” od ciągu?
Nie, trzeba inaczej.
Definicją granicy niewłaściwej jest:
Trzeba więc wyjść z nierówności
lub:
Ma Pan jakiś konkretny przykład?
Dzień dobry, mam problem z jednym przykładem z zadania, które dotyczy obliczenia granicy ciągu:
Nie do końca wiem, jak poradzić sobie z tymi pierwiastkami i potęgami przy wyciąganiu czegoś przed nawias. Bardzo proszę o pomoc 🙂
Pójdzie tak:
Czy można z definicji granicy udowodnić, że granicą (1-q^n)/(1-q) jest 1/(1-q)?
Można.
Trzeba na początek dodać, że zakładamy, że
(dla innych wartości 
granicą 
nie jest wcale 
).
Dowód
Musimy pokazać, że niezależnie jak bardzo małe
sobie obierzemy, od pewnych wartości 
“w górę”, czyli dla wszystkich 
większych od jakiegoś 
zachodzi zawsze nierówność:
Umawiamy się więc, że
i że bierzemy sobie jakieś dowolne 
. Nie określamy dokładnie jakie, bo 
musi być zupełnie dowolny.
Bierzemy się za nierówność:
Mianownik po lewej już jest wspólny, czyli:
Wartość bezwzględna po lewej jest równoważna:
Co do licznika, wiadomo, że
, ale nie możemy tak po prostu wartości bezwzględnej opuścić, bo 
, czyli 
może też przyjmować wartości ujemne dla pewnych 
.
Co do mianownika, skoro
, to 
jest zawsze dodatnie. Wartość bezwzględną możemy więc pominąć. Mamy:
Obie strony możemy pomnożyć przez
i na pewno nie zmieni to znaku nierówności (
).
Obie strony możemy zlogarytmować:
Prawdą jest też, że:
, czyli mamy:
Korzystając z własności logarytmu:
Teraz bardzo ważna rzecz. Dzieląc obie strony nierówności przez
wiemy, że dzielmy na pewno przez liczbę UJEMNĄ, ponieważ 
. Argument logarytmu jest więc mniejszy od 1, a z wykresu funkcji logarytmicznej wiemy, że dla takich argumentów wartości logarytmu są ujemne.
Skoro dzielimy przez liczbę ujemną, zmieniamy znak:
Pokazaliśmy więc, że nierówność
zachodzi wtedy i tylko wtedy, kiedy zachodzi nierówność 
.
Zastanówmy się, co z tego wynika.
Powiedzmy, że wybieramy sobie jakieś dowolne
. Dla tego wybranego przez nas, dowolnego, 
wyliczyć możemy sobie liczbę 
.
Skoro jednak pokazaliśmy, że
, oznacza to, że niezależnie jaka by ta 
nie była, od pewnych wartości 
będą one większe od 
.
A więc faktycznie:
Dowodzi to, że faktycznie granicą ciągu
przy 
jest 
.
Cześć, mam problem z policzeniem takiej granicy:lim
(
– 
)Bardzo proszę o pomoc 🙂
Cześć, a co jeśli wychodzi mi lim=2n/3? czyli nieskończoność/3, to wynikiem jest 0?
Jeśli wynik granicy wychodzi
to po podstawieniu otrzymujemy 
. Bierze się to stąd, że jakąś bardzo, bardzo dużą liczbę dzieli się przez 3, to i tak będzie ona nadal bardzo duża.
Granica zero wychodzi jedynie w przypadku, gdy w podstawieniu nieskończoność jest mianowniku, czyli
.
prosze o pomoc mam zad wyznaczyc dziedzine i zbior wartosci funkcji f(x)-2-4/x-3/
Serdecznie dziękuję :-). Wszystko wytłumaczone krok po kroku nic dodać nic ująć świetny blog! Pozdrawiam
Witam. Mam problem z obliczeniem granicy ciągu an= [1+2^2√2+3^2√(trzeciego stopnia)3+…+n^2√(ntego stopnia)n] / n(n+1)(n+2) . Proszę o pomoc.
Pozdrawiam, Paulina
Bardzo fajny artykuł ,ale mam problem z jedną rzeczą.W ostatnim przykładzie mamy podzielić obie strony przez (2e-1) i nie rozumiem dlaczego zmieniamy znak nierówności.Zgoda ,że dla pewnych wartości epsilon wyrażenie (2e-1) jest ujemne ale epsilon może przyjmować również wartości dla których to wyrażenie jest dodatnie ,a więc po podzieleniu i zmianie znaku nasza nierówność będzie dla pewnych wartości epsilon nieprawdziwa.
Pozdrawiam Ignacy
Ale już w następnym zdaniu artykułu biorę się do wyjaśniania, o co chodzi 🙂
Chodzi o to, że pokazuję, że nierówność NIE zachodzi dla pewnych wartości epsilon (np. takich, dla których 2e-1 jest ujemne), a z tego, że ta nierówność NIE zachodzi dla wszystkich epsilonów wynika, że liczba NIE jest granicą ciągu.
Rozumiem. Zastanawiałem się jeszcze tylko dlaczego nie rozpatrzył Pan dwóch przypadków albo nie wspomniał o tym ,że tak trzeba.W końcu olśniło mnie ,że nie trzeba tego robić bo jeżeli nasza nierówność może przyjmować różną postać w zależności od epsilona to zawsze lepiej wybrać tą mniejszą wartość bo jeżeli okaże się ,że równanie jest nie prawdziwe to mamy koniec zadania ,a jeżeli okazałoby się że nierówność jest prawdziwa to tym bardziej jest prawdziwa dla większych epsilonów choćby wartość graniczna N dla obydwu wartości epsilon była taka sama. Czy dobrze myślę?
Witam.
Mam problem z zadaniem:
Znajdź wszystkie możliwe wartości parametrów a,b,c należące do R, dla których
lim [((x^4+2x^3)^1/2)-ax^2-bx-c)=1 ( x towards infinity).
Proszę o pomoc.
Dobra, to powolutku pójdzie tak:
1. Trzeba cały czas pamiętać, że ogólnie granica ma wyjść równa 1, czyli: \underset{x\to \infty }{\mathop{lim }}\left( \sqrt{{{x}^{4}}+2{{x}^{3}}}-a{{x}^{2}}-bx-c \right)=1
2. Zaczynamy standardowym przekształceniem z mnożeniem przez sprzężenie (metodami pokazanymi w moim Kursie):
\underset{x\to \infty }{\mathop{lim }}\left( \sqrt{{{x}^{4}}+2{{x}^{3}}}-a{{x}^{2}}-bx-c \right)=\underset{x\to \infty }{\mathop{lim }}\left( \sqrt{{{x}^{4}}+2{{x}^{3}}}-\left( a{{x}^{2}}+bx+c \right) \right)\frac{\sqrt{{{x}^{4}}+2{{x}^{3}}}+\left( a{{x}^{2}}+bx+c \right)}{\sqrt{{{x}^{4}}+2{{x}^{3}}}+\left( a{{x}^{2}}+bx+c \right)}=
=\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{4}}+2{{x}^{3}}-{{\left( a{{x}^{2}}+bx+c \right)}^{2}}}{\sqrt{{{x}^{4}}+2{{x}^{3}}}+a{{x}^{2}}+bx+c}=\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{4}}+2{{x}^{3}}-\left( a{{x}^{2}}+bx+c \right)\left( a{{x}^{2}}+bx+c \right)}{\sqrt{{{x}^{4}}\left( 1+\tfrac{2}{x} \right)}+a{{x}^{2}}+bx+c}=
START =\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{4}}+2{{x}^{3}}-{{\left( a{{x}^{2}}+bx+c \right)}^{2}}}{\sqrt{{{x}^{4}}+2{{x}^{3}}}+a{{x}^{2}}+bx+c}=\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{4}}+2{{x}^{3}}-\left( a{{x}^{2}}+bx+c \right)\left( a{{x}^{2}}+bx+c \right)}{\sqrt{{{x}^{4}}\left( 1+\tfrac{2}{x} \right)}+a{{x}^{2}}+bx+c}=
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{4}}+2{{x}^{3}}-{{a}^{2}}{{x}^{4}}-ab{{x}^{3}}-ac{{x}^{2}}-ba{{x}^{3}}-{{b}^{2}}{{x}^{2}}-bcx-ca{{x}^{2}}-cbx-{{c}^{2}}}}{{\sqrt{{{{x}^{4}}\left( {1+\tfrac{2}{x}} \right)}}+a{{x}^{2}}+bx+c}}=
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{4}}\left( {1+\tfrac{2}{x}-{{a}^{2}}-\tfrac{{2ab}}{x}-\tfrac{{2ac}}{{{{x}^{2}}}}-\tfrac{{{{b}^{2}}}}{{{{x}^{2}}}}-\tfrac{{2bc}}{{{{x}^{3}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{4}}}}} \right)}}{{{{x}^{2}}\sqrt{{1+\tfrac{2}{x}}}+a{{x}^{2}}+bx+c}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{4}}\left( {1+\tfrac{2}{x}-{{a}^{2}}-\tfrac{{2ab}}{x}-\tfrac{{2ac}}{{{{x}^{2}}}}-\tfrac{{{{b}^{2}}}}{{{{x}^{2}}}}-\tfrac{{2bc}}{{{{x}^{3}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{4}}}}} \right)}}{{{{x}^{2}}\left( {\sqrt{{1+\tfrac{2}{x}}}+a+\tfrac{b}{x}+\tfrac{c}{{{{x}^{2}}}}} \right)}}=
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{2}}\left( {1+\tfrac{2}{x}-{{a}^{2}}-\tfrac{{2ab}}{x}-\tfrac{{2ac}}{{{{x}^{2}}}}-\tfrac{{{{b}^{2}}}}{{{{x}^{2}}}}-\tfrac{{2bc}}{{{{x}^{3}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{4}}}}} \right)}}{{\sqrt{{1+\tfrac{2}{x}}}+a+\tfrac{b}{x}+\tfrac{c}{{{{x}^{2}}}}}}=
Teraz ważny moment. Licznik, a wraz z nim cała granica, rozbiega do nieskończoności, CHYBA ŻE nawias \displaystyle {\left( {1+\tfrac{2}{x}-{{a}^{2}}-\tfrac{{2ab}}{x}-\tfrac{{2ac}}{{{{x}^{2}}}}-\tfrac{{{{b}^{2}}}}{{{{x}^{2}}}}-\tfrac{{2bc}}{{{{x}^{3}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{4}}}}} \right)}zbiega do zera, bo wtedy w liczniku jest wyrażenie nieoznaczone \left[ 0\cdot \infty \right].
Ponieważ wiemy, że cała granica nie ma rozbiegać do nieskończoności, tylko zbiegać do 1 (patrz punkt 1), nasz licznik MUSI być tym wyrażeniem nieoznaczonym, żebyśmy mieli na to szanse. Wyrażenie w nawiasie \displaystyle {\left( {1+\tfrac{2}{x}-{{a}^{2}}-\tfrac{{2ab}}{x}-\tfrac{{2ac}}{{{{x}^{2}}}}-\tfrac{{{{b}^{2}}}}{{{{x}^{2}}}}-\tfrac{{2bc}}{{{{x}^{3}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{4}}}}} \right)}musi więc zbiegać do zera. Składniki z x-sami w mianownikach już zbiegają, pozostaje nam 1-{a}^{2}, które powinno być równe zero. Stąd wniosek, że:
\displaystyle {{a}^{2}}=1
\displaystyle a=1 \vee a=-1
Mam więc dwa przypadki do rozpatrzenia, \displaystyle a=1i \displaystyle a=-1.
Zacznę od przypadku, że \displaystyle a=1:
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{2}}\left( {\tfrac{2}{x}-\tfrac{{2b}}{x}-\tfrac{{2c}}{{{{x}^{2}}}}-\tfrac{{{{b}^{2}}}}{{{{x}^{2}}}}-\tfrac{{2bc}}{{{{x}^{3}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{4}}}}} \right)}}{{\sqrt{{1+\tfrac{2}{x}}}+1+\tfrac{b}{x}+\tfrac{c}{{{{x}^{2}}}}}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{x\left( {2-2b-\tfrac{{2c}}{x}-\tfrac{{{{b}^{2}}}}{x}-\tfrac{{2bc}}{{{{x}^{2}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{3}}}}} \right)}}{{\sqrt{{1+\tfrac{2}{x}}}+1+\tfrac{b}{x}+\tfrac{c}{{{{x}^{2}}}}}}=
Tutaj sytuacja jest analogiczna. Licznik, a wraz z nim całe wyrażenie, rozbiega do nieskończoności, CHYBA ŻE wyrażenie w nawiasie, tzn. \displaystyle {x\left( {2-2b-\tfrac{{2c}}{x}-\tfrac{{{{b}^{2}}}}{x}-\tfrac{{2bc}}{{{{x}^{2}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{3}}}}} \right)}zbiega do zera.
Stąd analogiczny wniosek, że 2-2bmusi być równe zero, czyli:
b=1
Z tym założeniem liczę dalej:
=\underset{x\to \infty }{\mathop{lim }}\frac{x\left( -\tfrac{2c}{x}-\tfrac{1}{x}-\tfrac{2c}{{{x}^{2}}}-\tfrac{{{c}^{2}}}{{{x}^{3}}} \right)}{\sqrt{1+\tfrac{2}{x}}+1+\tfrac{1}{x}+\tfrac{c}{{{x}^{2}}}}=\underset{x\to \infty }{\mathop{lim }}\frac{-2c-1-\tfrac{2c}{x}-\tfrac{{{c}^{2}}}{{{x}^{2}}}}{\sqrt{1+\tfrac{2}{x}}+1+\tfrac{1}{x}+\tfrac{c}{{{x}^{2}}}}=\frac{-2c-1}{2}
Wiem, że wynik musi wyjść 1, zatem:
\frac{-2c-1}{2}=1
-2c-1=2
-2c=3
c=-\frac{3}{2}
Pierwsza odpowiedź więc to: odpowiedź więc, to: a=1,b=1,c=-\frac{3}{2}
Co potwierdza WolframAlpha:
http://www.wolframalpha.com/input/?i=lim_(x-%3Eoo)%20(sqrt(x%5E4%2B2x%5E3)-x%5E2-x%2B3%2F2)&t=crmtb01
Pozostaje oczywiście przypadek \displaystyle a=-1:
W tym przypadku granica będzie równa:
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{2}}\left( {\tfrac{2}{x}+\tfrac{{2b}}{x}+\tfrac{{2c}}{{{{x}^{2}}}}-\tfrac{{{{b}^{2}}}}{{{{x}^{2}}}}-\tfrac{{2bc}}{{{{x}^{3}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{4}}}}} \right)}}{{\sqrt{{1+\tfrac{2}{x}}}-1+\tfrac{b}{x}+\tfrac{c}{{{{x}^{2}}}}}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{x\left( {2+2b+\tfrac{{2c}}{x}-\tfrac{{{{b}^{2}}}}{x}-\tfrac{{2bc}}{{{{x}^{2}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{3}}}}} \right)}}{{\sqrt{{1+\tfrac{2}{x}}}-1+\tfrac{b}{x}+\tfrac{c}{{{{x}^{2}}}}}}=
Wyrażenie w nawiasie w liczniku \displaystyle {\left( {2+2b+\tfrac{{2c}}{x}-\tfrac{{{{b}^{2}}}}{x}-\tfrac{{2bc}}{{{{x}^{2}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{3}}}}} \right)}musi znowu zbiegać do zera, czyli musi być:
\displaystyle 2+2b=0
\displaystyle b=-1
Granica przyjmie wtedy postać:
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{x\left( {\tfrac{{2c}}{x}-\tfrac{1}{x}+\tfrac{{2c}}{{{{x}^{2}}}}-\tfrac{{{{c}^{2}}}}{{{{x}^{3}}}}} \right)}}{{\sqrt{{1+\tfrac{2}{x}}}-1-\tfrac{1}{x}+\tfrac{c}{{{{x}^{2}}}}}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{2c-1+\tfrac{{2c}}{x}-\tfrac{{{{c}^{2}}}}{{{{x}^{2}}}}}}{{\sqrt{{1+\tfrac{2}{x}}}-1-\tfrac{1}{x}+\tfrac{c}{{{{x}^{2}}}}}}
Tym razem zauważamy jednak, że mianownik dąży do zera (a nie do 2, jak w poprzednim przypadku). Aby całość dążyła do 1, licznik musi dążyć również do zera, powinno więc być:
\displaystyle 2c-1=0
\displaystyle c=\frac{1}{2}
Dla tak dobranego cwychodzimy na granicę:
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\tfrac{1}{x}-\tfrac{{\tfrac{1}{4}}}{{{{x}^{2}}}}}}{{\sqrt{{1+\tfrac{2}{x}}}-1-\tfrac{1}{x}+\tfrac{{\tfrac{1}{2}}}{{{{x}^{2}}}}}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{1-\tfrac{{\tfrac{1}{4}}}{x}}}{{x\left( {\sqrt{{1+\tfrac{2}{x}}}-1-\tfrac{1}{x}+\tfrac{{\tfrac{1}{2}}}{{{{x}^{2}}}}} \right)}}
Policzenie jej odpuszczę już sobie, ale można szybko sprawdzić w kalkulatorze, że równa jest nieskończoność (a nie 1):
Wynik tej granicy
Dla przypadku, gdy a=-1nie otrzymujemy więc rozwiązania.
Jedyną odpowiedzią jest: a=1,b=1,c=-\frac{3}{2}.
witam.
Jak udowodnić , że każdy ciąg ma conajmniej jedną granicę?
No ale to nieprawda, że każdy ciąg ma co najmniej jedną granicę…
Na przykład ciąg liczb naturalnych bez zera {{a}_{n}}=nnie ma żadnej granicy…
Ale ten ciąg ma granicę niewłaściwą – równą nieskończoność. Są inne ciągi, których granica nie istnieje.
witam, jak rozwiązać taką granice ciągu: (cosn^2/n^3+3n+1 ) -3 ?
Krystian!!! Jesteś wielki!!!! Dziękuję Ci…. Musiałeś nieźle się napracować… masz moje pokłony:)
No i teraz wszystko jasne 🙂 Super artykuł, baardzo pomocny. Dziękuję i pozdrawiam 🙂
Dzięki, pozdrawiam również.