Granica ciągu Wykład 1
Temat: Granica ciągu – intuicyjne wprowadzenie i definicja
Streszczenie
W artykule przedstawię, co to właściwie jest granica ciągu. Objaśnię też bliżej, jak rozumieć definicję tej granicy.
Co to jest ciąg?
Zanim przejdziemy do tego, czym jest granica ciągu, musimy sobie powiedzieć, czym ciąg właściwie jest. Ciągiem liczbowym nazwiemy liczby ustawione w kolejności, na przykład:
1,2,4,7,10
Powyżej mamy ciąg pięciowyrazowy. Istotna jest kolejność, na przykład:
2,1,4,7,10
To już zupełnie inny ciąg.
Jeśli mówić będziemy o granicy ciągu, pracować będziemy na ciągach nieskończonych, na przykład:
-4,-1,2,5,8,11,…
Przedstawiać ciągi można przez wypisywanie jego pierwszych kilku wyrazów, albo, o ile to możliwe, przez wypisanie wzoru na jego dowolny (na przykład setny) wyraz. Taki wzór dla ostatniego z wypisanych wyżej ciągów (-4,-1,2,5,8,11,…) wyglądał by tak:
Zmienna n we wzorze oznacza numerek wyrazu ciągu. Sprawdźmy czy się zgadza:
Pierwszy wyraz ciągu: 
– zgadza się (-4,-1,2,5,8,11,…)
Drugi wyraz ciągu: 
– zgadza się (-4,-1,2,5,8,11,…)
itd.
Przykłady ciągów. Ciągi zbieżne. Wyrazy ciągu na osi liczbowej.
W zrozumieniu, czym jest granica ciągu bardzo pomoże nam graficzne zaznaczanie wyrazów ciągu na osi liczbowej (pamiętajmy też, że od tej pory cały już czas mówimy o ciągach nieskończonych).
Weźmy na przykład nasz ciąg -4,-1,2,5,8,11,… (którego ogólny wyraz dany jest wzorem: (). Gdyby jego pierwsze wyrazy pozaznaczać na osi liczbowej wyglądała by ona tak:
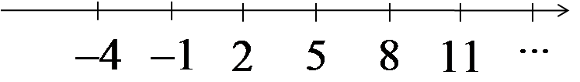
Zwróćmy uwagę, że gdyby jego kolejne wyrazy (14,17,…) zaznaczać na osi liczbowej NIE zbliżali byśmy się z nimi do jakiejkolwiek liczby na osi. Wręcz przeciwnie – “uciekalibyśmy” z nim coraz bardziej i bardziej w nieskończoność.
Teraz inny ciąg:
0,-2,-4,0,7,1,-2,2,2,…
Wyznaczenie wzoru ogólnego na n-ty wyraz tego ciągu jest raczej niemożliwe, bo jego wyrazy powstają dosyć chaotycznie i bez związku (choć są tacy, co uważają, że ZAWSZE jest jakiś wzór). Gdyby te wyrazy pozaznaczać na osi otrzymalibyśmy:
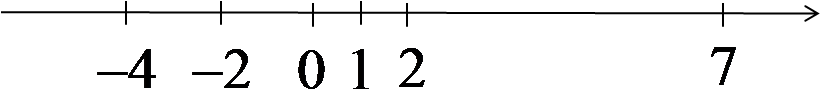
Zaznaczając kolejne wyrazy skakały by one to tu, to tam na osi NIE zbliżając się do jakiejkolwiek liczby. Są też i takie ciągi.
A teraz przyjrzyjmy się następującemu:
Można zauważyć, że w licznikach wyrazów są kolejne liczby naturalne, a w mianowniku liczby o 1 większe. Ogólnym wyrazem tego ciągu był by 
. Zaznaczając wyrazy takiego ciągu na osi zauważymy pewną rzecz:
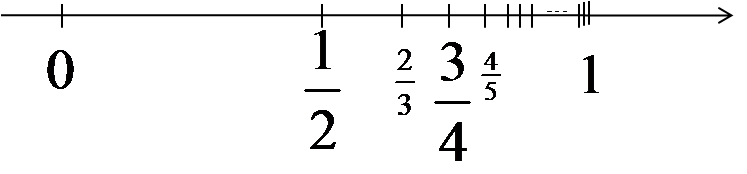Kolejne wyrazy tego ciągu były by coraz bliżej liczby jeden. Np. setny wyraz z kolei (możemy go policzyć podstawiając za n=100 we wzorze ) byłby równy 
. Bardzo blisko 1. Sto pierwszy były by jeszcze bliżej. Sto drugi jeszcze bardziej. Tysięczny: 
to już “prawie” jedynka. Biorąc coraz to większe numery wyrazów będziemy coraz bardziej “zbliżać się” do jedynki. Choć żaden konkretny wyraz ciągu nie będzie RÓWNY 1 (bo liczba podzielona przez liczbę większą od niej o 1 nie będzie równa nigdy 1), to powiedzieć można, że ciąg ten MA GRANICĘ równą 1.
To, co mamy to nieformalne, “intuicyjne” zrozumienie granicy ciągu. Nigdzie dokładnie i precyzyjnie nie zdefiniowałem, co to właściwie ściśle znaczy “dla coraz większych” (numerów wyrazów) i “coraz bliżej” (wyrazy do jakiejś liczby). Przejdziemy do tego w następnej części. Wyobraź sobie jednak, że tak mało ścisłe określenie granicy jakie tutaj mamy zupełnie wystarczało do różnych użytecznych rachunków na nieskończonościach przez długie, długie lata, zanim nie podano poprawnych i jednoznacznych definicji.
Zanim my zdefiniujemy ściśle “dla coraz większych … coraz bliżej…” musimy koniecznie powtórzyć sobie jedną rzecz, mianowicie jak oblicza się odległość dwóch punktów na osi (bo skoro ma być “coraz bliżej”, to musi się ona zmniejszać, prawda?).
Wzór na odległość dwóch punktów na osi liczbowej
Weźmy oś liczbową, a na niej dwie liczby (dla zmyłki jedną dodatnią, a drugą ujemną):
Wszyscy wiemy, że ta odległość to 6, ale jak to właściwie najszybciej obliczyć?
Można powiedzieć tak: trzeba od większej liczby odjąć mniejszą. W naszym przypadku od większej: 2 odjąć mniejszą:-4. Wynikiem będzie: 
. Zgoda. Ale przed odejmowaniem trzeba liczby porównywać i w zależności od porównania wykonywać różne działania. W przypadku odejmowania zmiennych, kiedy z góry nie jest określona, która z nich jest większa może to być kłopotliwe (trzeba by rozbijać na dwa możliwe przypadki).
Można więc powiedzieć inaczej: trzeba liczby odjąć (wszystko jedno, którą od której) a z wyniku obliczyć wartość bezwzględną (mam nadzieję, że wiesz, co to jest…). U nas moglibyśmy odjąć 2 od -4 i otrzymać: 
, lub odjąć -4 od dwóch: 
, czyli nasz wynik.
Odległość dwóch liczb od siebie na osi można więc obliczyć odejmując je w wartości bezwzględnej.
Nawróćmy teraz trochę do definicji granicy ciągu. Powiedzieliśmy tam sobie, że kolejne wyrazy ciągu (które, jak wiemy, można oznaczyć: 
) są “coraz bliżej” jakiejś liczby (nazwijmy ją: 
). Czyli, ujmując to innymi słowami, żeby odległość pomiędzy nimi była coraz mniejsza. Odległość, pomiędzy tymi dwoma rzeczami (n-tym wyrazem ciągu i liczbą ) możemy oznaczyć, jako:
I to właśnie powinno być coraz mniejsze, tzn. od pewnego wyraz dla coraz większych 
(numer wyrazu ciągu) powinno się zmniejszać.
Jak to zapisać formalnie?
Definicja granicy ciągu
Na początku wrzucę od razu formalną definicję, a później powolutku ją omówię dobra? Przypomnijmy jeszcze, że chodzi nam o to, żeby dla coraz większych było coraz mniejsze.
Definicja
Liczbę g nazywamy granicą ciągu, jeśli:
\underset{\varepsilon >0}{\mathop{\forall }}\,\underset{N}{\mathop{\exists }}\,\underset{n>N}{\mathop{\forall }}\,\left| {{a}_{n}}-g \right|<\varepsilonNo dobrze. Po pierwsze: jak ją w ogóle przeczytać? Znaczek: 
to odwrócona do góry nogami literka wielkie A, od angielskiego słowa “all”, czyli “każdy”. 
czytamy: “dla każdego epsilon większego od zera”.
Znaczek: 
to odwrócona do góry nogami literka wielkie E, od angielskiego słowa “exists”, czyli “istnieje”. 
czytamy: “istnieje takie N”.
Definicję przeczytamy więc następująco: “Dla każdego epsilon większego od zera istnieje takie N, że dla każdego n>N spełniony jest warunek: 
“.
Albo lepiej, przywołując, co właściwie znaczy n i :
” Dla każdego ustalonego przez nas (nawet bardzo małego) epsilona, istnieje taki numer wyrazu ciągu N, dla którego odległość wszystkich wyrazów ciągu o numerach większych od N jest mniejsza od epsilona”.
Czyli działa to na przykład tak:
Nawet jeśli za epsilon weźmiemy sobie bardzo, bardzo malutką liczbę, np. 
wszystkie wyrazy ciągu począwszy od np. 457 w górę (czyli wyraz numer 457, 458, 459 itd.) są oddalone od granicy ciągu o MNIEJ niż .
Spójrz, jak to zadziała w konkretnym przykładzie:
Przykład przybliżający definicję granicy ciągu
Weźmy nasz wypróbowany już ciąg:
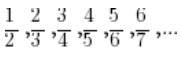, czyli:
Jeżeli ustawimy epsilon dosyć duże, np. 
, odległość każdego wyrazu ciągu począwszy od drugiego w górę (nasze N z definicji było by więc równe 1) od jedynki będzie mniejsza od epsilona, czyli od 0,5.
Jeżeli ustawimy epsilon mniejsze, na przykład 
, również stwierdzimy, że odległość każdego wyrazu ciągu począwszy od któregoś (konkretnie od czwartego, N=3) od jedynki będzie mniejsza od epsilona, czyli od 0,25.
Jeśli ustawimy epsilon jeszcze mniejsze, na przykład 
– również znajdziemy odpowiedni numer wyrazu, począwszy od którego odległości wyrazów od jedynki będą mniejsze od epsilona.
Historia powtórzy się, jak mały epsilon byśmy sobie nie przyjęli. Granica ciągu jest więc z definicji równa 1.
czytamy: “istnieje epsilon takie N”. – czytamy istnieje takie N
Poprawiłem, dzięki.
Witam! Mam problem z granicami przy których n pojawia sie w potedze, np.5 do n – 2 do n + 10 do n / 11 do n + 5 do n= ?????(Jest to 22 przyklad z zadania domowego z pierwszego wykladu o granicach)Jest jakis sposob na to? Pozdrawiam!
Akurat to jest Przykład 21 🙂
Rozwiązuję to podobnie jak w przypadku potęg, wyciągamy największa potęgę z licznika i mianownika (tym razem nie ma np
ale jest liczba do potęgi “n” – a największa jest ta, której podstawa jest największa, stąd:
Wiedząc, że
ostatecznie otrzymujemy wartość granicy:
potrzebuje o wyjaśnienie pewniej granicy. nie mam pojęcia jak się do niej zabrać.
Granicę obliczymy mnożąc przez sprzężenie licznika
w końcu zrozumiałam definicję granicy ciągu, której wcześniej musiałam uczyć się na pamięć 🙂 dzięki wielkie!
Witam, czy taką granicę rozwiązuję z twierdzenia o trzech ciągach? Niestety nie wiem którą metodę zastosować:(
pierwiastek z n, pod pierwiastkiem: 3^n (n^2+n+5) / 5^n * n
Niestety nie umiem inaczej wpisać pierwiastków i potęg z klawiatury. Serdecznie pozdrawiam i dziękuję z góry za odpowiedź! 🙂
Czy to miało być tak:
\underset{n\to \infty }{\mathop{lim }}\sqrt[n]{\frac{{{3}^{n}}\left( {{n}^{2}}+n+5 \right)}{{{5}^{n}}\cdot n}}[/latex]
?
Bo jeśli tak:
\underset{n\to \infty }{\mathop{lim }}\sqrt[n]{\frac{{{3}^{n}}\left( {{n}^{2}}+n+5 \right)}{{{5}^{n}}\cdot n}}=\underset{n\to \infty }{\mathop{lim }}\sqrt[n]{\frac{{{3}^{n}}}{{{5}^{n}}}\frac{{{n}^{2}}+n+5}{n}}=[/latex]
=\underset{n\to \infty }{\mathop{lim }}\sqrt[n]{{{\left( \frac{3}{5} \right)}^{n}}\left( n+1+\frac{5}{n} \right)}=\underset{n\to \infty }{\mathop{lim }}\sqrt[n]{{{\left( \frac{3}{5} \right)}^{n}}}\sqrt[n]{n+1+\frac{5}{n}}=[/latex]
=\underset{n\to \infty }{\mathop{lim }}\frac{3}{5}\sqrt[n]{n\left( 1+\frac{1}{n}+\frac{5}{{{n}^{2}}} \right)}=\underset{n\to \infty }{\mathop{lim }}\frac{3}{5}\sqrt[n]{n}\sqrt[n]{1+\frac{1}{n}+\frac{5}{{{n}^{2}}}}=\frac{3}{5}[/latex]
\underset{n\to \infty }{\mathop{lim }}\sqrt[n]{n}=1[/latex]– jest na to taki specjalny wzorek…
“Znaczek: “exists” to odwrócona do góry nogami literka wielkie E”
Chyba sam zrozumiesz gdzie jest błąd 🙂