Granice funkcji – definicja Heinego

Granice funkcji Wykład 5

Temat: Granice funkcji w punkcie – definicja Heine’go

Streszczenie

W artykule wprowadzę definicję granicy funkcji poprzez granicę ciągu. Jest to tzw. definicja Heinego granicy funkcji (jest także inna, Cauchy’ego – obie oczywiście równoważne). Przed przeczytaniem artykułu przydało by się wiedzieć jako tako, czym jest funkcja (przyporządkowanie jednych liczb innym), co to są argumenty, a co to wartości, jak rysować funkcję na wykresie (można wykonać prosty test: funkcja dla argumentu 3 przyjmuje wartość 4 – jak oznaczyć to na wykresie?), a także mieć jakie takie pojęcia o granicach ciągów, co to znaczy, że ciąg do czegoś zbiega itp.

Granica funkcji – o co mniej więcej chodzi?

Weźmy sobie taką (nietypową, ale dobrze w niej będzie widać, o co chodzi), funkcję:

Przypomnijmy może ze średniej, że ten dziwny zapis nie oznacza jakiś dwóch funkcji, lecz JEDNĄ funkcję, która argumentom mniejszym lub równym od 2 przyporządkowuje wartości według wzoru , a argumentom większym od 2 przyporządkowuje wartości według wzoru .

Na przykład ta funkcja argumentowi przyporządkuje wartość  (bo 1 jest mniejsze od 2, czyli skorzystałem ze wzoru ).

Argumentowi ta funkcja przyporządkuje wartość (bo 3 jest większe od 2, czyli skorzystałem ze wzoru ).

Tabelka argumentów i wartości tej funkcji mogła by wyglądać tak:

Dla argumentów x mniejszych lub równych od 2 wartości y liczyłem ze wzoru , a dla argumentów x większych od 2 wartości y liczyłem ze wzoru .

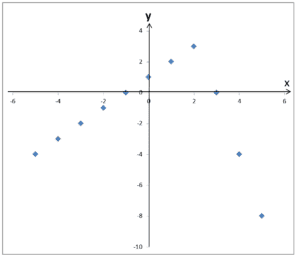
Zaznaczając otrzymane argumenty i wartości na wykresie otrzymam:

Przechodząc do standardowego już “łączenia kropek” (mogę to zrobić, bo funkcja przyjmuje jakąś wartość dla wszystkich argumentów mniejszych lub równych 2, a nie tylko tych “okrągłych” -5,-4,-3 itd.) napotkam się na pewien problem. Na lewo od argumentu dwa mamy cały czas ten sam wzór i możemy naszkicować tam wykres:

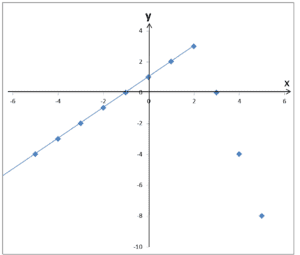
i co dalej? Łącząc bezmyślnie i mechanicznie kropki otrzymamy zupełnie nieprawidłowy wykres:

Przykładając zaś linijkę do trzech kropek na prawo od 2 orientujemy się, że coś jest nie tak, bo wykres powinien wtedy wyglądać:

… i tak wygląda rzeczywiście. Przekonajmy się o tym na liczbach (wyciągnij kalkulator). Dla wszystkich argumentów x większych od 2 obowiązuje nas wzór .

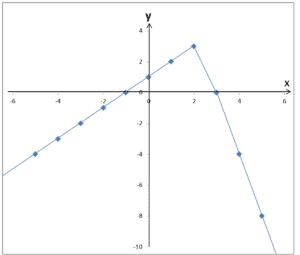
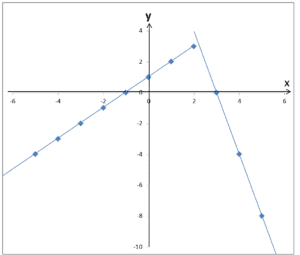
Czyli dla argumentu wartość funkcji równa będzie .

…widać wyraźnie, że dla obranego przeze mnie ciągu argumentów x: 2,5;2,25;2,1;2,01;2,001 dążącego do liczby 2, odpowiadający im ciąg wartości: 2; 3; 3,6; 3,96; 3,996 dąży do 4 (ale nigdy dokładnie 4 nie osiąga).

Zaznaczając teraz kropki na wykresie wyglądało by to tak:

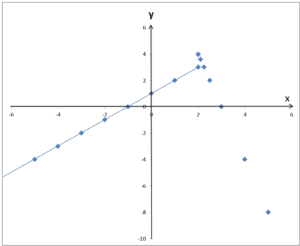
…a łącząc je:

…gdzie kółeczko podkreśla, że wykres dążąc do wartości cztery nigdy dokładnie jej nie osiąga.

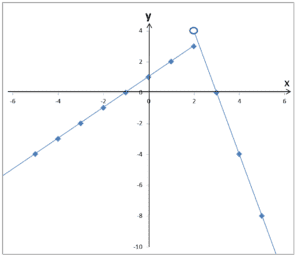
No i tyle. Takie sytuacje właśnie, kiedy argumenty zbiegają do jakiejś liczby (powiedzmy ) i odpowiadające im wartości funkcji również zbiegają do jakiejś liczby (powiedzmy ) oznaczają, że funkcja osiąga w punkcie  granicę równą .

Nie takie trudne, prawda? Niestety, musimy to – ale tylko troszeczkę – skomplikować.

Granice lewo i prawostronne funkcji

W naszym przykładzie należy jeszcze rozróżnić sytuację, w której ciąg argumentów zbiega do 2 z prawej strony (wtedy odpowiadający im ciąg wartości zbiega do 4), od tej, w której ciąg argumentów zbiega do 2 ze strony lewej, wtedy odpowiadający im ciąg wartości zbiega do 3 (możesz się o tym przekonać biorąc na przykład ciąg argumentów: 1,5; 1,75; 1,9; 1,99; 1,999, podstawiając do wzoru , bo te argumenty są mniejsze od 2 i sprawdzając, że odpowiadające im wartości dążą do 3).

Mówimy więc, że funkcja osiąga w 2 granicę prawostronną równą 4 i granicę lewostronną równą 3.

Gdyby obie te granice, tzn. lewo i prawostronna były równe, można by było powiedzieć jednym zdaniem: “funkcja osiąga w 2 granicę równą …” w miejsce kropek wstawiając oczywiście wartość tej granicy.

Definicja granicy funkcji

Pokuśmy się więc teraz o formalne zdefiniowanie granicy funkcji (na początku granicy prawostronnej). Jest to tzw. definicja Heinego. Wykorzystuje ona definicję granicy ciągu, granicy ciągu już nie definiujemy (bo zakładamy już, że wiemy co to znaczy, że “ciąg zbiega”):

Liczbę g nazywamy granicą prawostronną funkcji w , jeśli

Czytamy:

Jeśli dla każdego ciągu argumentów dążącego z prawej strony do , odpowiadający im ciąg wartości dąży do , liczbę nazywamy granicą funkcji w punkcie .

Tu podkreślmy super ważną rzecz, o jakiej jeszcze nie mówiliśmy w tym naszym opisywaniu “mniej więcej” granicy funkcji. Są to te dwa słowa” “dla każdego”. Ciąg argumentów dążący do  musi być dowolny.

W naszym przykładzie ja wybrałem sobie jakiś przykładowy, konkretny ciąg argumentów dążący do 2 i pokazałem (powiedzmy…), że odpowiadający im ciąg wartości zbiega do 4. W sensie formalnym NIE dowiodło by jednak to w żaden sposób, że funkcja ma w 2 granicę prawostronną równą 4. Takim dowodem było by dopiero to, gdybym pokazał, że dla DOWOLNEGO ciągu argumentów (a nie tylko pierwszego z brzegu, jaki sobie wybrałem) dążącego do dwóch z prawej strony ciąg wartości zbiega do 4.

Formalna definicja granicy lewostronnej funkcji wygląda – jak się domyślamy – zupełnie analogicznie:

Liczbę g nazywamy granicą lewostronną funkcji w , jeśli

Czytamy:

Jeśli dla każdego (jeszcze raz: dla każdego) ciągu argumentów dążących do z lewej strony odpowiadający im ciąg wartości funkcji dąży do .

A jak zdefiniować ogólną granicę funkcji w punkcie (bez rozróżnienia, czy jest to granica lewo, czy prawostronna)?

Liczbę g nazywamy granicą funkcji w , jeśli:

Czyli:

Jeśli dla dowolnego ciągu argumentów dążących do odpowiadające im ciągi wartości zbiegają do tej samej liczby , oznacza to, że funkcja osiąga granicę równą w punkcie .

Podkreślmy jeszcze raz, że granica funkcji istnieje, kiedy granice lewo i prawostronne funkcji są sobie równe. Zatem na przykład funkcja z naszego przykładu NIE osiąga granicy w punkcie 2 (choć osiąga w nim granice lewo i prawostronne).

KONIEC

Kliknij, aby przypomnieć sobie, czym są granice niewłaściwe ciągu (poprzedni Wykład) <–

Kliknij, zobaczyć, jak inaczej zdefiniować można granice funkcji (następny Wykład) –>

Kliknij, aby powrócić na stronę z wykładami o granicach