Wykazywanie, że liczba jest (bądź nie jest) granicą funkcji z definicji

Granice funkcji Wykład 7

Temat: Wyznaczanie granic funkcji z definicji

Streszczenie

W artykule pokażę na kilku przykładach wykazywać z definicji (Cauchy’ego lub Heine’go), że liczba jest, lub nie jest granicą funkcji. Przed przystąpieniem do czytania artykułu potrzebne jest zrozumienie obu definicji granic funkcji – opierającej się na granicach ciągu definicji Heine’go i opierającej się na otoczeniach punktu definicji Cauchy’ego.

Granice funkcji Cauchy’ego – przykład 1

Wykaż z definicji, że liczba  jest granicą funkcji  przy x dążącym do 1.

Innymi słowy, mamy wykazać, że:

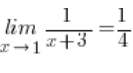
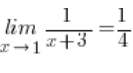
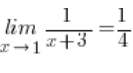
Do wykazania użyjemy definicji granic funkcji Cauchy’ego. Przypomnijmy ją:

Liczbę g nazywamy granicą funkcji w punkcie , jeśli:

W naszym konkretnym przykładzie mamy:

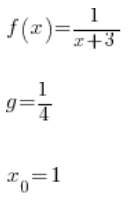
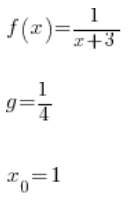
Mamy więc pokazać, że niezależnie od tego, jak małe sobie nie obierzemy, zawsze znajdziemy do niego takie , że z nierówności:  wynikać będzie nierówność .

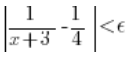
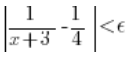
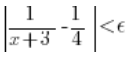
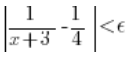
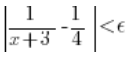
Weźmy więc dowolny    i nierówność:

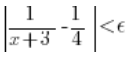
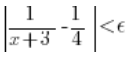
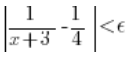
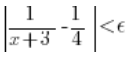
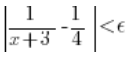
Jeszcze raz zwróćmy uwagę na ważną rzecz. Dobór konkretnego  w nierówności: zależy tylko od nas, możemy go sobie wybrać jaki nam się tylko podoba, ważne jest tylko, żeby dla tego naszego wyboru zachodziło: .

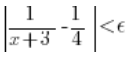
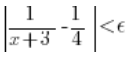
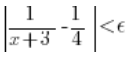
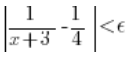
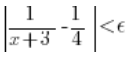
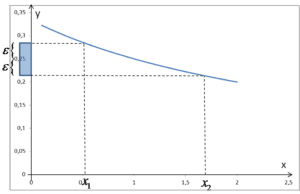
Zilustrujmy sprawę na rysunku. Mamy obrane dowolnie małe otoczenie wartości – o szerokości  (odpowiada to nierówności ):

Na osi argumentów OX trzeba teraz dobrać takie otoczenie 1, żeby wartości odpowiadające temu otoczeniu zawsze zawierały się w otoczeniu zaznaczonym powyżej. Ważną rzeczą jest, że można to zrobić dowolnie. Można więc zrobić tak:

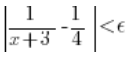
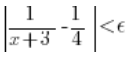
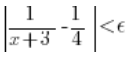
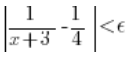
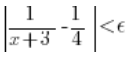
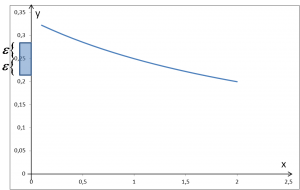
Najpierw wyznaczymy  i   takie, że jak na rysunku:

Jak się do tego zabrać? Widać z rysunku, że wartość funkcji w punkcie musi byś równa , a wartość funkcji w punkcie  musi byś równa . Czyli:

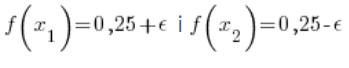
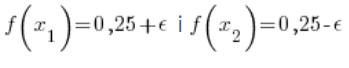
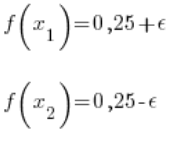
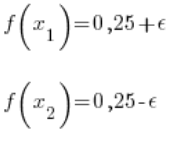
Wzorem na wartość funkcji jest , zatem:

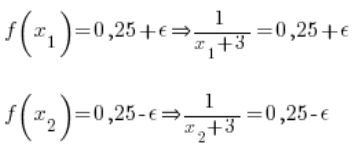
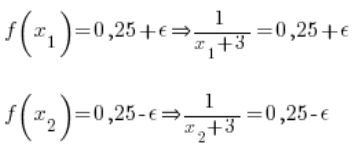
Rozwiązuję równanie pierwsze:

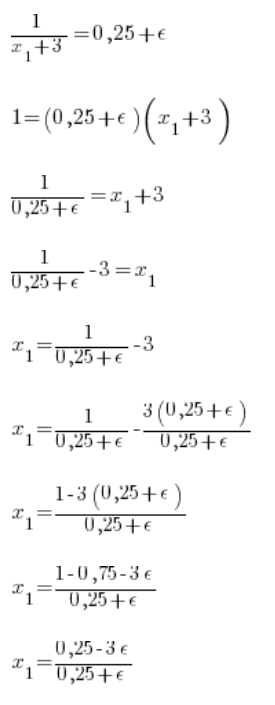
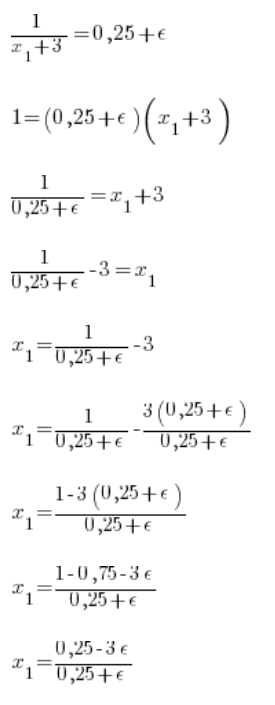
Mam policzone . Analogicznie liczę :

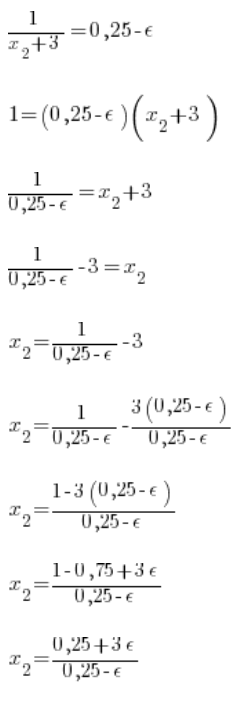
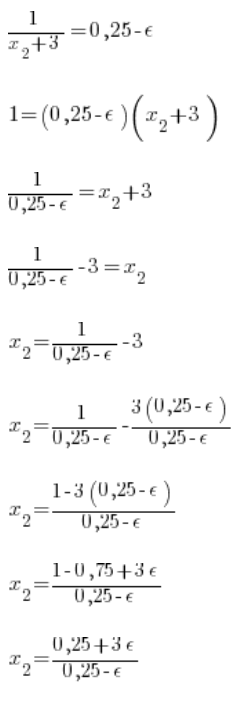
Mamy więc policzone . Nanoszę te wartości na rysunek:

Nasze dowolne otoczenie argumentów 1 powinno zawierać się w przedziale pomiędzy    i . – wtedy odpowiadające mu otoczenie wartości na pewno będzie zawierać się w otoczeniu wartości z epsilonem (zaznaczonym na rysunku na niebiesko). Jakie wybrać?

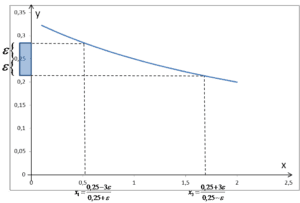
Bierzemy otoczenie o długości od 1 do lub – w zależności od tego, które z nich jest bliżej 1. W naszym przykładzie będzie to (na końcu pokażę Ci, jak robić to bardziej ogólnie). Zaznaczam to otoczenie na rysunku:

Na rysunku zaznaczyłem też – które obieram właśnie w ten sposób (jeszcze raz podkreślam, że zupełnie arbitralnie – byle zawierało się pomiędzy i ). Policzymy je za chwilę (od 1 trzeba będzie odjąć ), a na razie zwróćmy uwagę, że dla tego wybranego przez nas otoczenia spełniona odpowiadające mu otoczenie wartości zawiera się w tym wyjściowym z epsilonem:

Z rysunku widać, że nasze obliczymy tak:

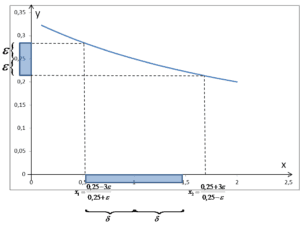
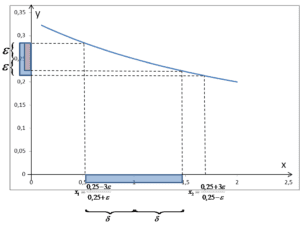
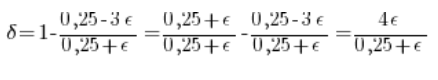
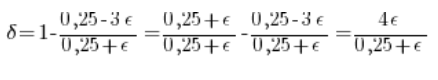
Jasne jest, że powyższe rozumowanie można by przeprowadzić niezależnie od wyboru na początku. Czyli dla każdego dobierzemy takie , że spełniony będzie warunek:

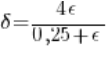
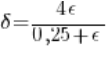
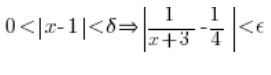
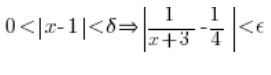
Zatem funkcja w punkcie  ma granicę równą . Pokazaliśmy, że:

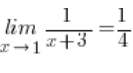
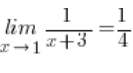
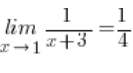
Granice funkcji Cauchy’ego – przykład ogólny

Uogólniając sposób wykorzystywany w powyższym przykładzie (tak, żeby nie trzeba było np. rysować wykresu funkcji) aby wykazać, że funkcja osiąga granicę  g  w punkcie   z definicji Cauchy’ego, można:

1. Rozwiązać równania:

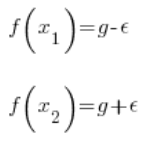
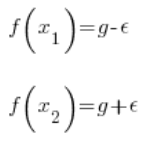
2. Przyjąć za :

– czyli mniejszą spomiędzy odległości między a krańcami przedziału i (w przykładzie powyżej wynikało jasno z rysunku, która z nich jest mniejsza).

Granice funkcji Cauchy’ego – przykład 2

Wykaż z definicji Cauchy’ego, że liczba  nie jest granicą funkcji  przy x dążącym do 1.

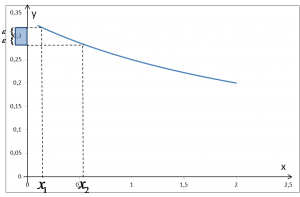
Zilustrujmy. Mamy dowolnie małe otoczenie wartości :

i mamy pokazać, że nieprawdą jest, że dla każdego takiego otoczenia znajdziemy takie otoczenie argumentu 1, że odpowiadające mu otoczenie wartości zawierać się będzie w wybranym na początku.

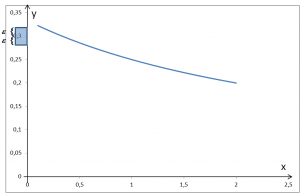
Z logicznego punktu widzenia: mamy pokazać, że istnieje takie otoczenie wartości 0,3, dla którego nie znajdziemy żadnego otoczenia argumentu 1, że odpowiadające mu otoczenie wartości zawiera się w początkowym otoczeniu wartości 0,3. Ujmując to bardziej szpanersko: negacja odwraca kwantyfikatory.

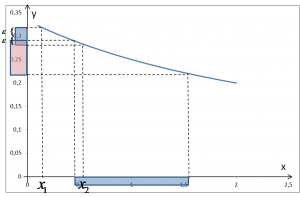
Nie będzie to trudne. Spójrzmy na rysunek:

Widać, że choćbyśmy stawali na głowie, nie dobierzemy takiego otoczenia 1, żeby odpowiadające mu otoczenie wartości zawierało się w początkowym:

Widać rysunku, że wystarczy wziąć byle jakie , Przyrównać  do  i wyznaczyć epsilon. Pokażemy w ten sposób, że istnieje taki , dla którego nie istnieje takie , że:

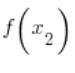
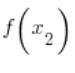
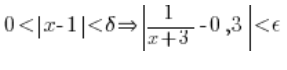
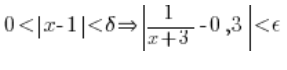
…a będzie to znaczyło, że funkcja nie osiąga granicy równej 0,3 w punkcie 1.

Do dzieła zatem. Biorę sobie (arbitralnie)

Czyli obliczyć muszę równanie:

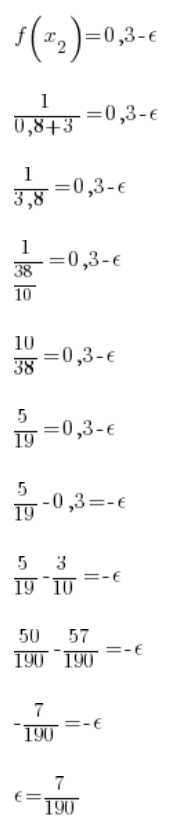
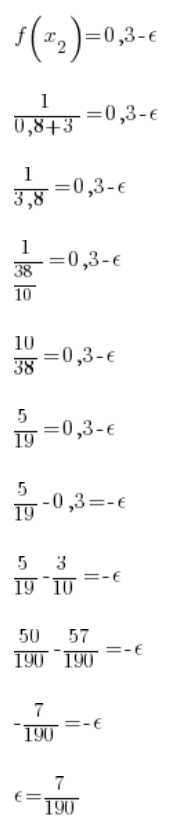
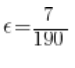
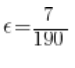
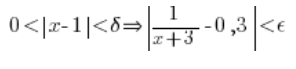
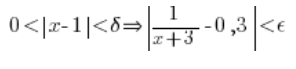
Zatem istnieje taki epsilon (), dla którego nie istnieje takie , że:

Czyli pokazaliśmy, że funkcja nie osiąga granicy równej 0,3 w punkcie 1.

Granice funkcji Heine’go – przykład 3

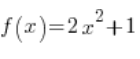
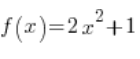
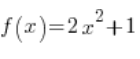
Korzystając z definicji granicy funkcji Heine’go wykaż, że granicą funkcji  w punkcie 2 jest liczba 9.

Należy więc wykazać, że:

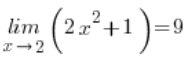
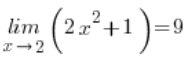
…korzystając z definicji granic funkcji Heine’go.

Przypomnijmy definicję:
Liczbę g nazywamy granicą funkcji w , jeśli:

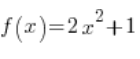
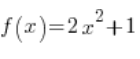
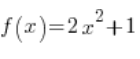
W naszym zadaniu będziemy wykazywać, że dla dowolnego ciągu wyrazów dążącego do 2, odpowiadający mu ciąg wartości funkcji dąży zawsze do 9.

Uwaga: nie wystarczy, że weźmiemy sobie jakiś byle jaki ciąg dążący do 2, np.  i pokażemy, że odpowiadający mu ciąg wartości:  zbiega do 9. Nie wystarczy, bo definicja wymaga, aby ta zależność zachodziła “zawsze”, dla dowolnego ciągu. Nie wystarczy wiec, że pokażemy, że zachodzi w jakimś konkretnym, wybranym ciągu.

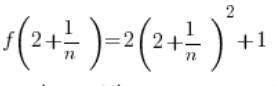
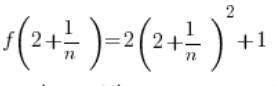
Bierzemy więc:

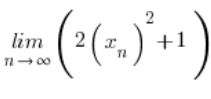
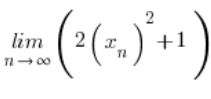
Jeżeli ciąg dąży do 1 powyższa granica nie jest symbolem nieoznaczonym. Z własności ciągów zbieżnych (mnożenie ciągów zbieżnych) wiemy, że:

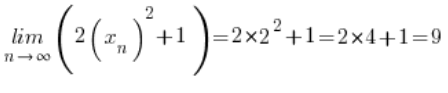
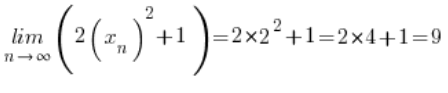
dla dowolnego ciągu dążącego do 1.

Dowodzi to, że dana funkcja osiąga granicę równą 9 w punkcie 2.

Granice funkcji Heine’go – przykład 4

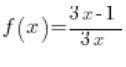
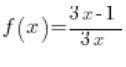
Korzystając z definicji granicy funkcji Heine’go wykaż, że granicą funkcji  w punkcie 1 nie jest liczba 2.

Definicja granicy funkcji mówi nam, że dla każdego ciągu argumentów dążących do 1 odpowiadający im ciąg wartości powinien dążyć do 2 – żeby 2 była granicą funkcji w 1.

Aby pokazać coś odwrotnego, czyli to, że 2 nie jest granicą funkcji w 1 musimy więc pokazać, że istnieje taki ciąg argumentów dążący do 1, że odpowiadający mu ciąg wartości nie dąży do 2 – logiczne, prawda?

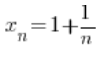
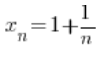
Bierzemy więc na przykład bardzo typowy ciąg argumentów dążący do 1:  ( dąży do 0 ze wzoru: stała podzielić przez nieskończoność).

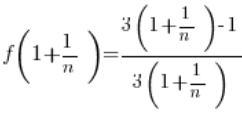
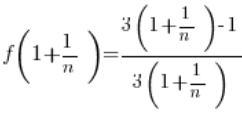
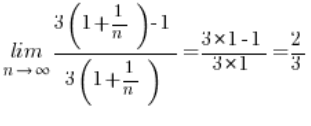
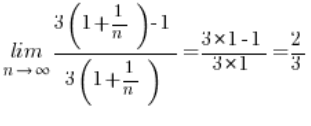
Odpowiadający mu ciąg wartości funkcji wyglądać będzie następująco: . Jego granica…

…nie jest równa 2.

Nie jest więc prawdą, że dla każdego ciągu argumentów dążących do 1 odpowiadający im ciąg wartości dąży do 2 (bo znaleźliśmy taki ciąg argumentów, że odpowiadający im ciąg wartości dąży do , a nie do 2).

Zatem pokazaliśmy, że dana funkcja nie osiąga granicy równej 2 w punkcie 1.

Porównanie definicji

Czy tylko ja odnoszę wrażenie, że definicja Heinego jest szybsza, bardziej zrozumiała i wygodniejsza do praktycznych zastosowań? 🙂

KONIEC

Kliknij, aby przypomnieć sobie, jaka była definicja Cauchyego granicy funkcji (poprzedni Wykład) <–

Kliknij, aby zobaczyć, jak definicję granicy funkcji zastosować do wykazania trudniejszej granicy (następny wykład) –>

Kliknij, aby powrócić na stronę z wykładami o granicach