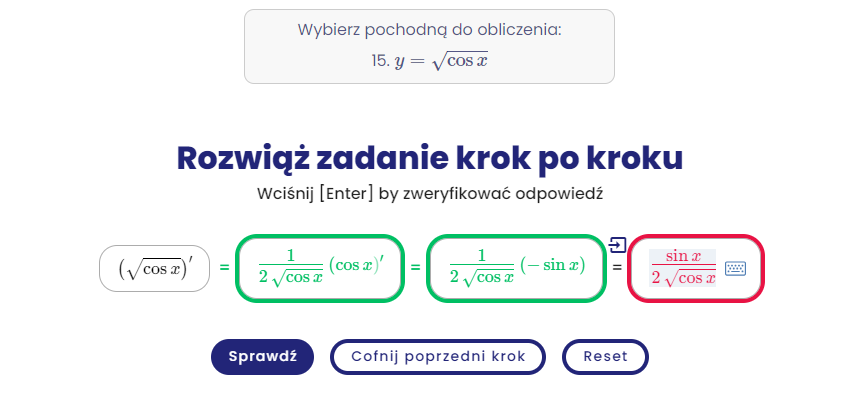
Kalkulator do granic funkcji dwóch zmiennych (NIEAKTUALNE) + nowy kalkulator
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Ogłoszenie
Niestety, po wielu latach od udostępnienia przeze mnie darmowego kalkulatora do granic funkcji dwóch zmiennych, musiałem go “wyłączyć”.
Kalkulator był prostym “widgetem” strony WolframAlpha. Jakiś czas temu Wolframalpha zmienił swoją politykę odnośnie widgetów. Między innymi: przestały one obliczać “na miejscu”, tylko przerzucają użytkownika na stronę WolframAlpha .
Przepraszam za kłopot wszystkich dotychczasowych użytkowników Kalkulatora Do Granic Funkcji.
Nowy kalkulator granic funkcji dwóch zmienncy
Zapraszam też do nowego kalkulatora granic funkcji, stworzonego już przeze mnie. Dostęp do niego oraz do innych interaktywnych narzędzi możecie uzyskać w ramach subskrypcji za jedyne 5,99 zł / miesiąc (lub taniej w opcjach kilkumiesięcznych) na stronie:
A sam kalkulator wygląda tak:
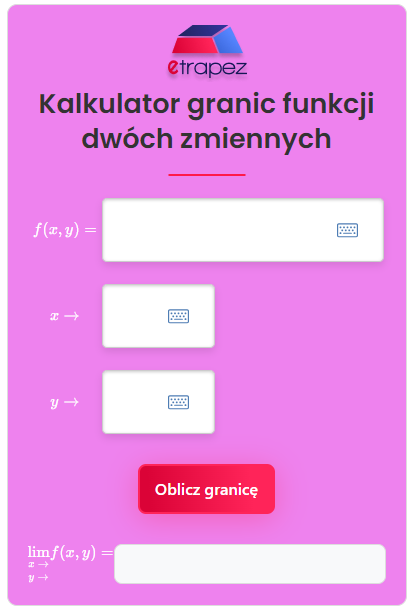
Pozdrawiam i powodzenia!
Krystian Karczyński
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.