Funkcje Cyklometryczne Wykład
Temat: Funkcje cyklometryczne
Streszczenie
Na wykładzie wprowadzę pojęcie funkcji cyklometrycznych: arcsinx, arccosx, arctgx, arcctgx. Są to funkcje odwrotne do funkcji trygonometrycznych.
Wykład składa się z dwóch części. W pierwszej pokazuję tylko jak szybciutko liczyć wartości funkcji cyklometrycznych, bez zbytniego wgłębiania się w temat (do tej części dołączony jest filmik Video, fragment mojego Kursu Całek Oznaczonych, Niewłaściwych i Zastosowań Całek ).
W drugiej opisuję funkcje cyklometryczne bardziej ściśle, pokazuję ich wykresy itd.
Do zrozumienia wykładu potrzebne będą:
- funkcje trygonometryczne (szkoła średnia)
Część I
Funkcje cyklometryczne – wersja „INSTANT”
Funkcje cyklometryczne „na chłopski rozum” to po prostu funkcje odwrotne do trygonometrycznych. Czyli arcsinx to funkcja odwrotna do sinx.
Czyli jeśli np. wiemy, że 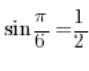 , to znaczy, że
, to znaczy, że ![]() .
.
I tak dalej:
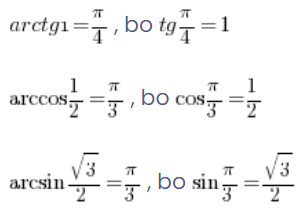
Do tego mamy jeszcze parę własności funkcji cyklometrycznych, które pozwalają nam obliczać ich wartości także dla argumentów ujemnych:
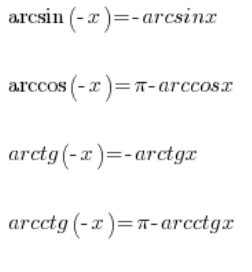
Możemy sobie więc jeszcze policzyć do tego:
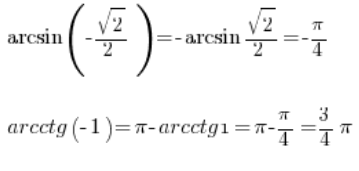
Mając więc tabelkę funkcji trygonometrycznych spokojnie wyznaczymy z niej wartości funkcji cyklometrycznych, odczytując ją po prostu „na odwrót”.
Objaśniam to dokładniej tu na filmiku:
Tabelka podstawowych wartości funkcji trygonometrycznych z filmiku – pobierz tutaj .
Część II
Funkcje cyklometryczne – pełna wersja
Wstęp – dlaczego w sumie część I to za mało
Wygląda więc na to, że w części I zdefiniowaliśmy każdą funkcję cyklometryczną jako odwrotną do odpowiadającej jej trygonometrycznej.
Sformalizujmy to trochę. Powiedzieliśmy, że np. funkcja ![]() przyjmuje wartość
przyjmuje wartość ![]() , gdy funkcja
, gdy funkcja ![]() z tego
z tego ![]() równa jest
równa jest ![]() .
.
Odpowiednio:
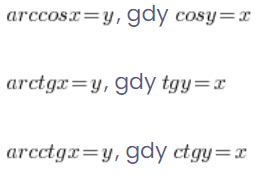
Czyli jeśli chcemy obliczyć ![]() zastanawiamy się, cosinus jakiego kąta daje
zastanawiamy się, cosinus jakiego kąta daje ![]() , wpadamy na to, że jest to kąt
, wpadamy na to, że jest to kąt ![]() i mamy wynik:
i mamy wynik: 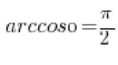 .
.
Czy to już wyczerpuje nam temat wartości funkcji cyklometrycznych?
Oczywiście NIE.
Prześledźmy jeszcze raz całe rozumowanie na konkretnych liczbach (i przerzućmy się może tradycyjnie na arcsinx):
Jeśli chcemy obliczyć  zastanawiamy się, sinus jakiego kąta daje
zastanawiamy się, sinus jakiego kąta daje ![]() , wpadamy na to, że jest to kąt
, wpadamy na to, że jest to kąt ![]() i mamy wynik:
i mamy wynik:  .
.
Gdzie tu problem? W pogrubionym fragmencie:
Jeśli chcemy obliczyć  zastanawiamy się, sinus jakiego kąta daje
zastanawiamy się, sinus jakiego kąta daje ![]() , wpadamy na to, że jest to kąt
, wpadamy na to, że jest to kąt ![]() i mamy wynik:
i mamy wynik:  .
.
Niestety, nie tylko sinus ![]() równy jest
równy jest ![]() .
.
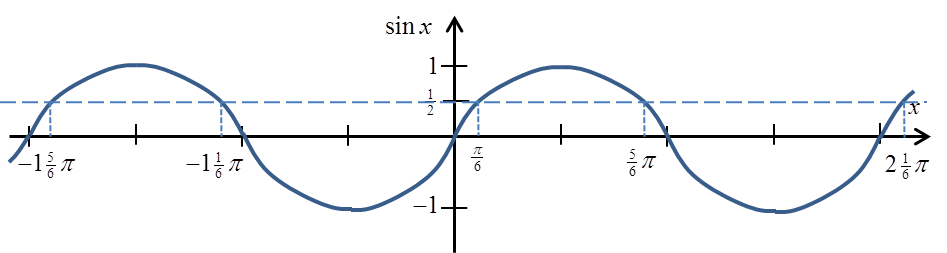
Przypomnijmy wykres funkcji sinx (zaznaczyłem na nim wartość ![]() ):
):
Widać i wiemy to już ze szkoły średniej, że sinus osiąga wartość ![]() nie tylko dla kąta
nie tylko dla kąta ![]() , ale także dla kątów:
, ale także dla kątów: 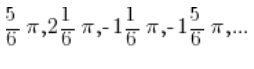
Czyli 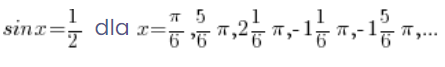
Przypomnijmy więc jeszcze raz nasz sposób obliczania arcsin:
Jeśli chcemy obliczyć  zastanawiamy się, sinus jakiego kąta daje
zastanawiamy się, sinus jakiego kąta daje ![]() , wpadamy na to, że jest to kąt
, wpadamy na to, że jest to kąt ![]() i mamy wynik:
i mamy wynik:  .
.
No ale teraz wiemy już, że nie tylko sin![]() daje
daje ![]() , wygląda więc na to, że:
, wygląda więc na to, że:
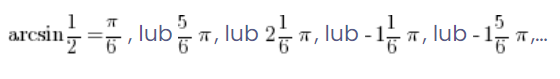
To oznaczało by, że arcsinx nie jest w ogóle funkcją, bo jednemu argumentowi przyporządkowanych jest kilka wartości!
Udzielenie jednoznacznej odpowiedzi na pytanie, ile równy jest arcsin z czegoś było by wtedy zupełnie niemożliwe.
Łatwo też sobie wyobrazić, że podobny problem dotyczy KAŻDEJ z funkcji trygonometrycznych.
Nazywając rzecz bardziej fachowo: te funkcje nie są różnowartościowe, zatem funkcje odwrotne do nich nie istnieją. W każdej z funkcji trygonometrycznych każda ich wartość zostaje osiągnięta dla nieskończonej liczby argumentów (są one okresowe, prawda?), zatem przy próbie wyznaczenia ich funkcji odwrotnych otrzymamy nieskończoną liczbę wartości przyporządkowaną do każdego argumentu. A tak w funkcjach nie może być.
Co robić?
To dosyć proste, żeby nie powiedzieć: prostackie. Każdą z funkcji trygonometrycznych można OBCIĄĆ tak, aby w rezultacie otrzymać funkcję różnowartościową.
Do dzieła zatem, zdefiniujmy już prawidłowo wszystkie 4 funkcje cyklometryczne:
arcsinx
Przypomnijmy wykres funkcji sinx:
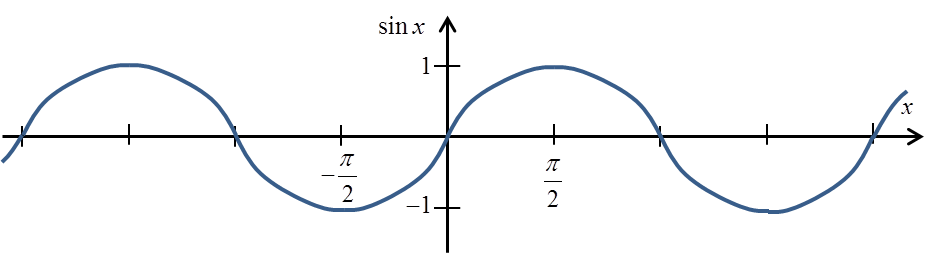
Jeśli umówimy się, że obetniemy go na przykład do przedziału do przedziału ![]() , otrzymamy taki wykres:
, otrzymamy taki wykres:
![Wykres sinx w przedziale [0,pi] Obraz3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
Nie jest to niestety to, o co nam chodzi, ponieważ nie jest dalej wykres funkcji różnowartościowej i problem z wartością np. ![]() nadal występuje:
nadal występuje:
![Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2 Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
Umawiamy się więc, że funkcję sinx przycinamy inaczej, do argumentów 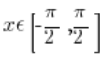 :
:
![Wykres funkcji sinx dla x należących do [-pi/2,pi/2] Wykres funkcji sinx dla x należących do [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
Teraz jest to funkcja różnowartościowa i istnieje do niej funkcja odwrotna arcsinx.
Wykres funkcji arcsinx wyglądać będzie mniej więcej tak:

Jej dziedziną jest przedział ![]() nie istnieje.
nie istnieje.
Ścisłe określenie funkcji arcsinx to zatem:
![]() .
.
arccosx
Funkcja cosx również nie jest funkcją różnowartościową:
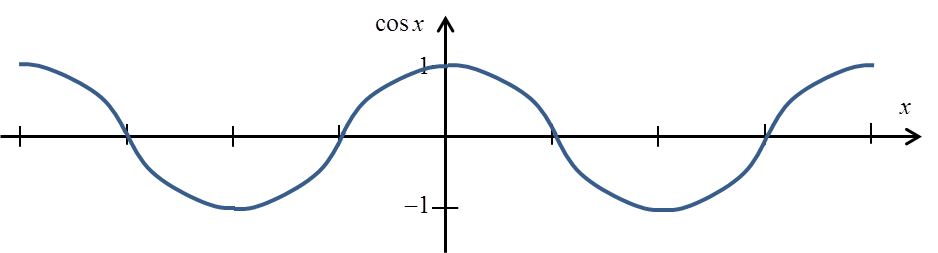
Aby otrzymać funkcję różnowartościową musimy go jednak przyciąć do przedziału ![]() :
:
![Wykres funkcji cosx obciętej do przedziału [0,pi] Wykres funkcji cosx obciętej do przedziału [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
Tak określona funkcja jest już różnowartościowa i posiada funkcję odwrotną arccosx.
Jej wykresem będzie mniej więcej:
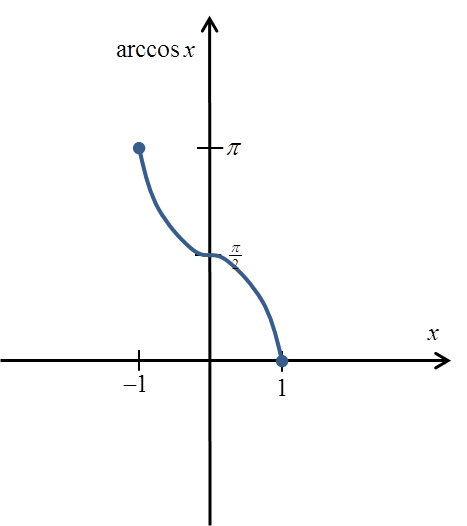
A jej ścisłym określeniem:
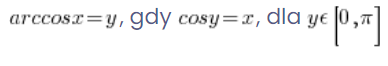 .
.
arctgx
Wykres funkcji tgx wygląda tak:

Również nie jest funkcja różnowartościowa! Obciąć możemy go w następujący sposób:
![Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2] Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
Otrzymując w ten sposób funkcję różnowartościową.
Wykres funkcji arctgx wygląda tak:

A jej ścisłe określenie jest takie:
![]() , dla y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
, dla y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
Zauważmy też, że z wykresu wynika kilka ciekawych własności, np:
- dziedziną funkcji arctgx jest cały zbiór liczb rzeczywistych (arctg policzymy z każdej liczby)


arcctgx
Z wykresu funkcji ctgx:

Wykrajamy różnowartościowy kawałek:
Wykres funkcji arcctgx wygląda tak:
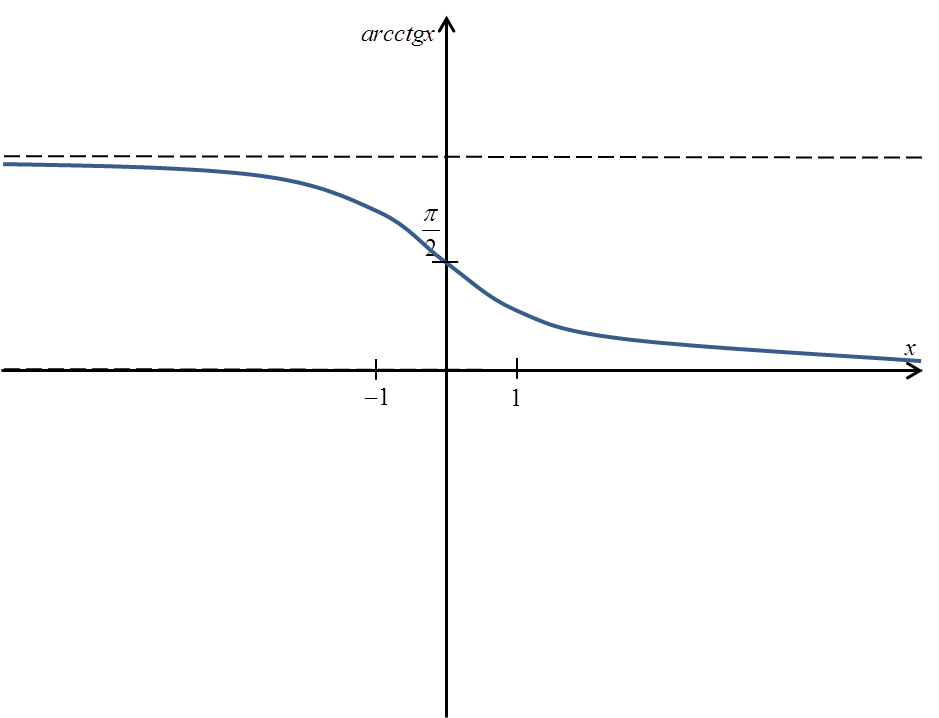
Ścisłe określenie arcctgx było by takie:
![]() .
.
Widać, że:
- dziedziną funkcji arcctgx jest cały zbiór liczb rzeczywistych (arcctg policzymy z każdej liczby)


Uwaga
W wielu kalkulatorach i w ogóle zapisach matematycznych (zwłaszcza zachodnich) funkcje odwrotne do trygonometrycznych nie oznacza się jako „arcus”, tylko wykładnikiem potęgi -1. Na przykład arcsinx zapisuje się jako ![]() . Jak się wie, o co chodzi, to nie ma problemu. Można jednak zrobić makabryczny błąd i pomylić funkcję odwrotną do sinx z funkcją
. Jak się wie, o co chodzi, to nie ma problemu. Można jednak zrobić makabryczny błąd i pomylić funkcję odwrotną do sinx z funkcją ![]() – która jest jeszcze zupełnie inną od arcsinx funkcją.
– która jest jeszcze zupełnie inną od arcsinx funkcją.


Integral Love
Biedny arcus secans i arcus cosecans ;-;
Treka
Powiem w skrócie. Jesteś niesamowity!
Iwona Marczewska
Doskonałe wyjaśnienie! Nie wyobrażam sobie studiowania bez uzupełniania wiedzy na eTrapez 🙂
Uwielbiam matematykę, ale nie potrafię się jej uczyć sama i potrzebuję dokładnie tego, co tu znajduję. 🙂 Dziękuję!
Magda
Witam chciała bym sie dowiedziec o 5 własności funkcji arctgx . Pozdrawiam
Joanna Grochowska
Funkcja arctgx jest:
– rosnąca
– nieparzysta
– różnowartościowa
– ciągła
– różniczkowalna
– jej dziedziną jest \displaystyle Re , a przeciwdziedziną \displaystyle \left( {-\frac{\pi }{2},\frac{\pi }{2}} \right)
jessica
Przy rysunku arctg jest wpisany arcctg i jako nagłówek tez arcctg zamiast arctg
Krzysztof Banach
jak dla mnie kozak, czeto korzystam z Pana lekcji, dziękuje i pozdrawiam
Panajotis
ctg(-x) = – ctg x na filmiku jest błąd ;(
Krystian Karczyński
Zgadza się, w tabelce zamiast ctg(-x) = ctgxpowinno być ctg(-x) = – ctgx.
Przepraszam za swoją pomyłkę.
Mateusz
Czy przeciwdziedzina funkcji arcctg to nie zbiór (0;PI)? A nie [0,PI]?
Krystian Karczyński
Tak, oczywiście, przepraszam. Poprawiłem.
Marta
Czy wykres ctg na pewno jest poprawny? Funkcja ta przyjmuje dla 45 stopni jeden a ni minus jeden.
Krystian Karczyński
Nie był poprawny, przepraszam (szkoła średnia się kłania…)! Już poprawiłem.
Marta
Strasznie ubolewam nad faktem że nie mam szans na tak wyśmienitego prowadzącego na studiach jak Pan 🙂
Matematyka przedstawiana na zajęciach jest przerażająca – jednak, gdy przeczytam/ pooglądam Pana prezentacje wszystko staje się jaśniejsze. Dziękuje 🙂
Ola
Świetnie! Bardzo Panu Dziękujemy, bardzo mi się to przyda. Pozdrawiam serdecznie:)