Sustituciones de Euler de Primer Tipo

---

Sustituciones de Euler – ¿a quién le importa?

Las sustituciones de Euler en integrales indefinidas son lo siguiente que se introduce después de las integrales racionales, integrales trigonométricas y integrales con raíces (o según algunas clasificaciones: “integrales irracionales”). Lo que significa que la mayoría de los estudiantes no tendrán el placer de encontrarse con ellas, tampoco las incluí en mi Curso de Integrales Indefinidas.

Sin embargo, hay un grupo bastante grande de estudiantes en carreras de matemáticas, o realmente, realmente “fuertes” en matemáticas, que tendrán que lidiar con las sustituciones de Euler, y a esos (y a los interesados) les invito. Discutiré los tres tipos de sustituciones de Euler (en este post abordaré el primer tipo) y haré un ejemplo de cada uno.

Vamos allá.

¿Qué integrales resolvemos con las sustituciones de Euler?

Con las sustituciones de Euler resolvemos integrales del tipo:

…es decir, algunos enlaces arbitrarios y . Así que se pueden tratar como una especie de “extensión” del tema de las integrales con raíces (“irracionales”).

Resolvemos con las sustituciones de Euler las integrales que no se pueden resolver más fácilmente, por supuesto. Por ejemplo, la integral:

es una integral en la que tenemos la relación y , pero se puede resolver muy fácilmente con una simple sustitución: . Así que no disparamos un cañón a un gorrión y en tales integrales sencillas no nos complicamos con Euler.

Pero tomemos la integral:

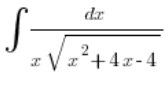
Vemos que la situación es más seria, las sustituciones conocidas anteriormente , o (no podemos extraer de ellas ).

Necesitamos un nuevo arma.

Sustituciones de Euler – Primer Tipo

Al tener una integral:

en la cual ,

aplicamos la sustitución:

, elevamos ambos lados al cuadrado, los términos se cancelan (y eso es lo que buscamos), determinamos (en orden):

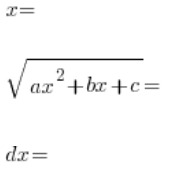
, expresados en términos de t, y los sustituimos en la integral original:

y obtenemos una integral en términos de t (si todavía nos quedan x-ses, hemos cometido un error) y es una integral racional.

Nota

Es importante añadir que, en la práctica, muchos estudiantes solo aprenden las sustituciones de Euler del Primer Tipo y solo para integrales del tipo:

, es decir, aquellas en las que como si

Veamos las sustituciones de Euler de Primer Tipo en acción, en el ejemplo:

Ejemplo 1

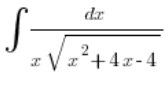
Observamos que es una integral en la que existe una relación entre y . Que no se puede resolver simplemente. Que ( es obviamente el coeficiente junto a , en nuestro ejemplo es igual a 1).

Así que procederemos con la sustitución de Euler de Primer Tipo.

Sustituimos:

es decir, simplemente:

elevamos ambos lados al cuadrado:

Los términos con en ambos lados se cancelan (y eso es lo que buscamos en cada ocasión):

Y ahora es cuando necesitamos determinar , y (en ese orden).

Empezamos por :

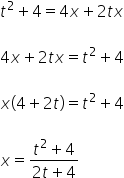
Tenemos expresado en términos de t. Ahora es el turno de , o sea, en nuestro ejemplo: .

Volvemos a nuestra primera sustitución, donde estaba:

Ahora que ya conocemos (se ve por qué es importante el orden, ¿verdad?), podemos escribir:

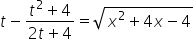
es decir:

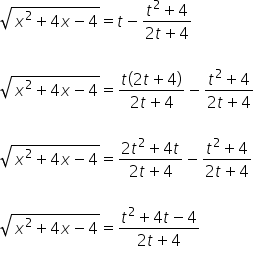
Así que tenemos expresado en términos de la variable .

Finalmente, tomamos , que obtenemos simplemente diferenciando ambos lados del determinado:

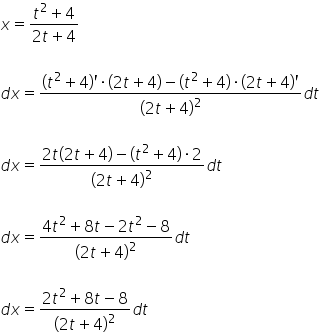
Y de esta manera determinamos . Así que tenemos:

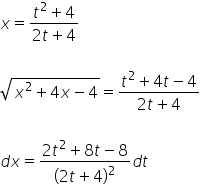
Insertamos todo esto en la integral original:

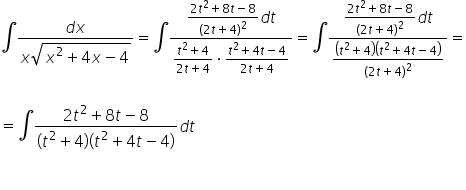
A primera vista, esto parece una tediosa, pero ya conocida y esquemática integral racional (descomposición en fracciones simples, el segundo factor en el denominador se puede descomponer aún más). Por lo general, así es, pero en este ejemplo concreto tendremos un poco de suerte y nos ahorraremos pasar por 3 páginas de cálculos A4:

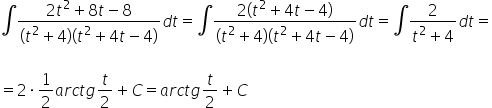
¿Cómo volvemos a la sustitución? Al principio teníamos:

De ahí, por supuesto:

Así que nuestro resultado es:

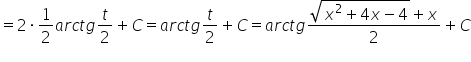
Continuará. (aún tenemos dos tipos más de sustituciones de Euler, ¿qué pasa si el coeficiente no es mayor que cero?).