No hay productos en el carrito.
Krystian Karczyński- 2 agosto 2024
- Komentarz 0
Sustituciones de Euler de los Tipos I, II, III – No se Necesita Más
En publicaciones anteriores, mostré cómo usar las sustituciones de Euler en integrales del tipo:
- Sustituciones de Euler de Primer Tipo (cuando a>0)
- Sustituciones de Euler de Segundo Tipo (cuando c>0)
En esta publicación, nos ocuparemos del tercer y último tipo de sustituciones de Euler, que podemos usar cuando en la integral:
el polinomio cuadrático 
, tiene dos raíces distintas 
, es decir, cuando su 
, es decir, cuando se puede escribir en forma factorizada: 
.
Pero antes de llegar a los hechos, notemos que estos tres casos:
- Primer tipo, cuando a>0
- Segundo tipo, cuando c>0
- Tercer tipo, cuando hay dos raíces distintas
nos permitirán resolver cualquier integral del tipo:
De hecho, incluso solo el primer y tercer tipo son suficientes.
¿Por qué?
El caso cuando 
podemos ignorarlo, porque el polinomio cuadrático simplemente se convierte en una forma lineal 
, que podemos resolver con sustituciones más simples que las de Euler.
¿Pero qué pasa con el caso cuando a<0 (no encaja con el primer tipo) y el polinomio cuadrático tiene una o ninguna raíz en absoluto (no encaja con el tercer tipo)?
Entonces su gráfico se vería así (recordemos de la escuela – brazos hacia abajo):
o, si no tuviera ninguna raíz, así:
¿Qué conclusión podemos sacar? Que en ambos casos el polinomio cuadrático tomaría valores negativos (excepto como máximo un punto), y les recuerdo que estamos calculando la integral:
Es decir, en la función bajo la integral, el polinomio cuadrático está bajo la raíz, y esta no se puede calcular a partir de valores negativos (obviamente, estamos trabajando con números reales). Es decir, el dominio de dicha función sería como máximo un punto, lo que no tiene sentido, y ciertamente no obtendremos un ejemplo así. A menos que el profesor esté realmente muy cansado al preparar los ejemplos para el examen.
Entonces, el caso cuando a<0 y el polinomio cuadrático no tiene dos raíces se puede ignorar, y ahora es claro que los tipos I y III de sustituciones de Euler se ajustan a cualquier integral del tipo:
Entonces, vamos a proceder con el tercer tipo de sustituciones de Euler.
Sustituciones de Euler de Tercer Tipo
Tenemos una integral:
,
donde tiene , es decir, se puede escribir como:
,
donde son sus raíces.
La sustitución que usamos aquí es:
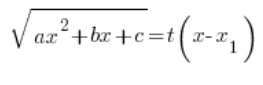
Cuadramos ambos lados de esta sustitución, escribimos el polinomio cuadrático en el lado izquierdo en forma factorizada (sabemos que se puede), dividimos ambos lados por 
y continuamos como en los tipos anteriores de sustituciones, determinando en secuencia:
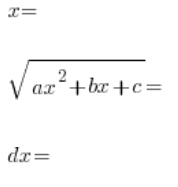
Finalmente, sustituimos todo en la integral original y terminamos con una integral racional – generalmente tediosa.
Vamos a empezar.
Ejemplo
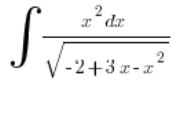
Nuestro 
(es decir, a<0, por lo tanto no usaremos sustituciones de primer tipo), nuestro 
(es decir, c<0, por lo tanto no usaremos sustituciones de segundo tipo), pero nuestro 
, es decir, podemos usar sustituciones de tercer tipo.
Calculamos primero :
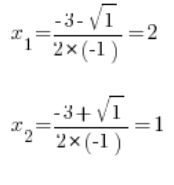
Usamos la sustitución de Euler de tercer tipo:
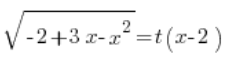
Cuadramos ambos lados:
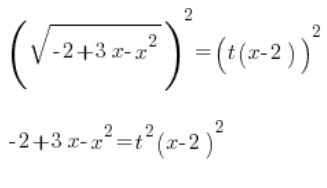
Escribimos el polinomio cuadrático en el lado izquierdo en forma factorizada (recuerden 
aquí!!!):
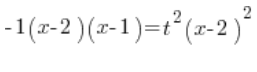
Dividimos ambos lados por 
:
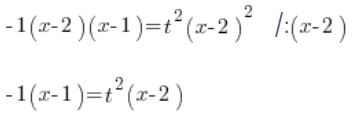
Determinamos 
:
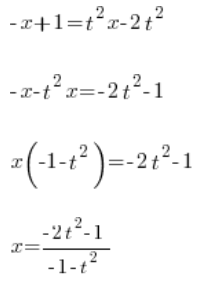
Tenemos determinado usando la variable 
. Ahora determinamos 
.
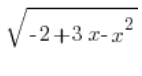Volviendo a nuestra primera sustitución, tenemos que:
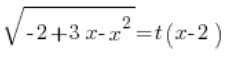
Sustituimos lo determinado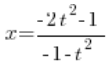 
, y tenemos:
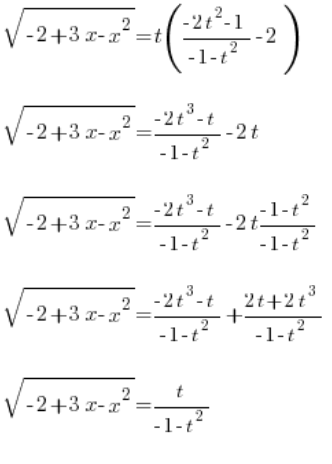
Tenemos 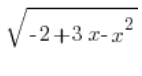determinado bastante bien. Ahora solo falta 
, que calculamos encontrando la derivada de :
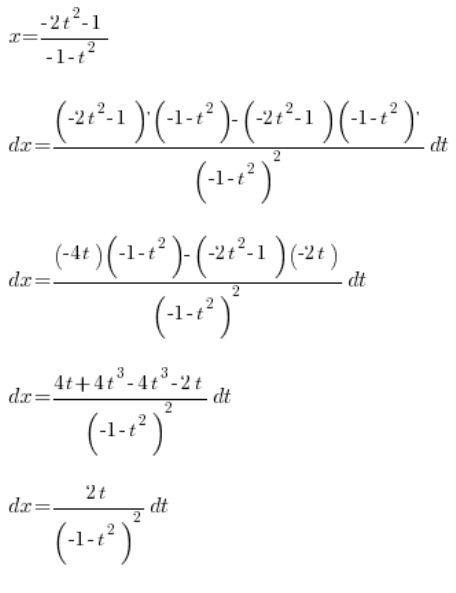
Así que hemos determinado:
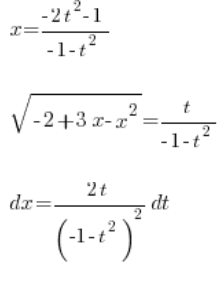
, todo usando la variable . Ponemos esto en la integral:
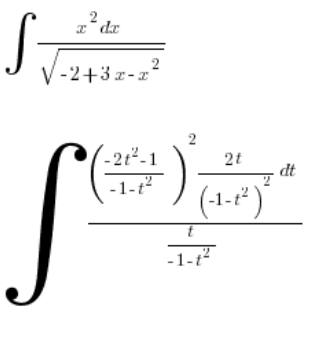
Simplificamos:
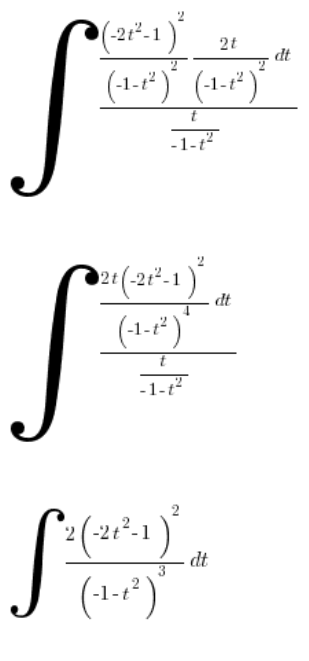
Como era de esperar, llegamos a una integral racional bastante tediosa, que no voy a calcular.
Finalmente, vale la pena señalar que…
Nota sobre las Sustituciones de Euler
Tenemos una integral:
,
donde:
- Primer tipo, cuando a>0
- Segundo tipo, cuando c>0
- Tercer tipo cuando hay dos raíces distintas
Es obvio que a menudo se puede resolver usando una de las dos sustituciones de Euler, o incluso cualquiera de ellas (cuando a>0, c>0 y al mismo tiempo ).
No hay problema, aunque por facilidad de cálculo recomendaría usar primero el primer tipo, si eso no funciona, luego el segundo, y si eso tampoco funciona, finalmente el tercer tipo.
Eso es todo sobre el uso de las sustituciones de Euler, espero que les sea útil en sus estudios, y como siempre, siéntanse libres de comentar debajo de la publicación.
