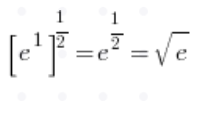Límites típicos de sucesiones con una fórmula para el número e
Los problemas tradicionales sobre límites de sucesiones con una fórmula para el número e conducen de manera bastante «natural» a la fórmula (muestro cómo hacerlo en mi Curso):
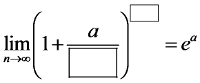¿Pero qué pasa si en lugar de esa fracción tan elegante, tenemos algo como esto en los paréntesis:
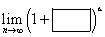Si el rectángulo en los paréntesis tiende a cero, y el triángulo en el exponente tiende a infinito, tenemos un símbolo indeterminado 
– exactamente el tipo en el que usamos la fórmula con el número ‘e’ en el resultado. ¿Qué hacer?
Bueno, recordemos que cualquier expresión se puede representar como dividir uno por el recíproco de esa expresión 🙂
Por ejemplo, el número 2 se puede escribir como:
Así que, cualquier expresión se puede «forzar» a ser una fracción si es realmente necesario.
Ejemplo de un límite no convencional con una fórmula para el número e
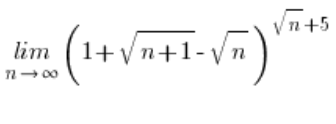
Primero, deberíamos demostrar que la expresión 
tiende a cero. Puedes hacerlo calculando el límite:
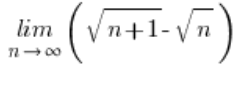– el resultado será realmente cero (puedes usar el método de multiplicación por el conjugado).
Ahora, reemplaza:
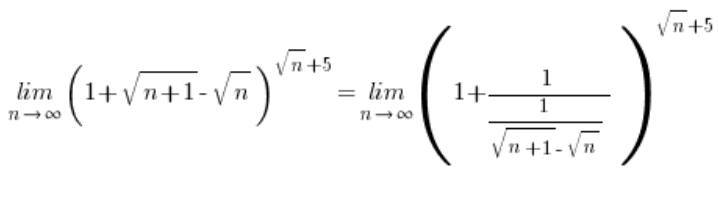
… y continúa según el esquema conocido:
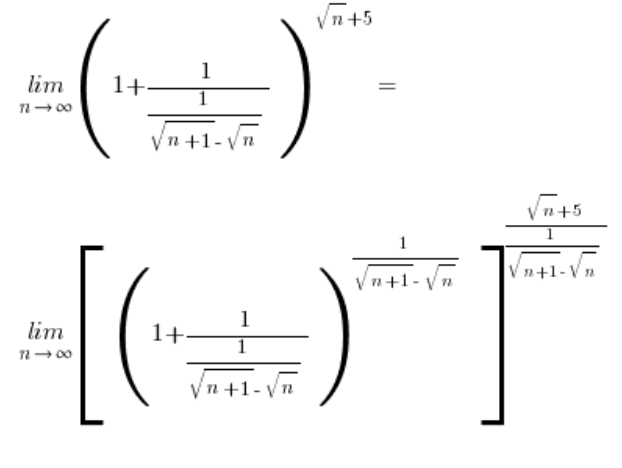
El límite en el gran paréntesis cuadrado es: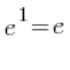 
– según la fórmula básica fórmula, solo queda el último paso:
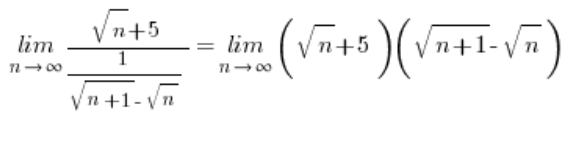
… que, después de aplicar la multiplicación por el conjugado, terminará con el resultado 
.
Así que, todo el límite es igual a:
