Tomemos el siguiente límite de una secuencia:
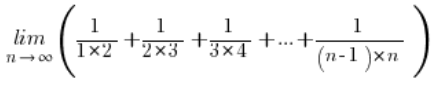
En el problema, sentimos que necesitamos usar fórmulas de suma de secuencias (aritméticas o geométricas) pero desafortunadamente, desafortunadamente… Esta secuencia no es ni aritmética ni geométrica…
¿Qué hacer?
Tenemos que hacerlo de una manera completamente diferente. Descomponer cada fracción en fracciones simples. Esto se hace bastante intensamente cuando se trata de integrales indefinidas de funciones racionales por ejemplo. La idea es encontrar constantes A y B tales que…
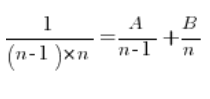
Multiplicamos ambos lados de la ecuación anterior por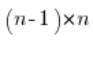 
, obteniendo:
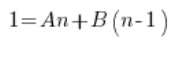
Luego:
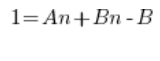
Comparamos los coeficientes de los polinomios en el lado izquierdo y derecho (igualdad de polinomios – escuela secundaria) y obtenemos un sistema de ecuaciones:
De la segunda ecuación: 
.
Sustituyendo esto en la primera ecuación:
También tenemos 
.
Así que podemos descomponer cualquier fracción en:
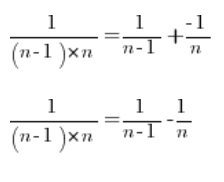
Volviendo a nuestro límite de la secuencia y descomponiendo cada fracción en fracciones simples:
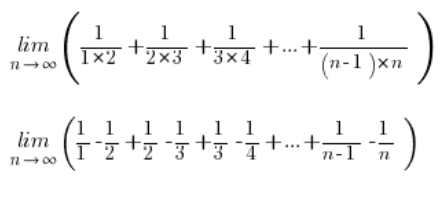
Simplificando algunos términos, nos queda:
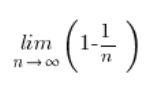
Y este límite de la secuencia ya no es aterrador, por supuesto:
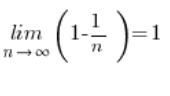
P.S.
Puedes encontrar muchos ejemplos interesantes de límites de secuencias en mi Curso en Video dedicado a los límites.
