Integrales definidas calculadas con respecto a la variable y

Krystian Karczyński

Fundador y jefe del servicio eTrapez.

Maestro en Matemáticas por la Universidad Tecnológica de Poznań (Polonia). Tutor de matemáticas con muchos años de experiencia. Creador de los primeros Cursos eTrapez, que se han vuelto enormemente populares entre estudiantes de toda Polonia.

Vive en Szczecin (Polonia). Le gusta caminar por el bosque, ir a la playa y hacer kayak.

Las integrales definidas se pueden calcular con respecto a la variable x o y, y a veces deberían hacerse así si es más conveniente. Esto juega un papel importante a menudo en las aplicaciones de las integrales, como: calcular el área de regiones, longitudes de arco, volúmenes y áreas superficiales de sólidos de revolución. A menudo ni siquiera tenemos opción, porque las condiciones del problema especifican que la curva gira alrededor del eje OY, no el OX.

¿Cómo hacerlo?

Primero, necesitas hacer un dibujo y marcar el área/longitud del arco/volumen que necesitas calcular. Sin esto, no podemos comenzar.

Segundo, debes determinar los límites de integración en el eje OY (de manera similar a como se hace en el eje OX).

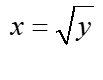Ahora, todo lo que necesitas hacer es determinar las curvas límite para los datos (generalmente) con respecto a la variable x usando la variable y, por ejemplo, si tenemos la curva , determinamos “x” y así obtenemos dos funciones de la variable y: y .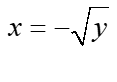

Luego simplemente creamos la integral apropiada con límites de integración en el eje OY y funciones de la variable y, por ejemplo, en el área de la región sería:

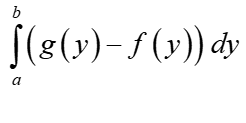
¡Repetiré de nuevo, la base es un gráfico claro y grande!