No hay productos en el carrito.
Krystian Karczyński- 3 agosto 2024
- Komentarz 0
Continuidad de una función en un punto
Como todos sabemos (aunque sea por mi Curso de Límites), la función 
es continua en el punto 
, cuando:
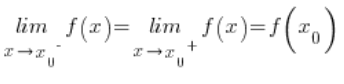
Es decir, cuando el límite por la izquierda de esta función en ese punto es igual al límite por la derecha de la función en ese punto, y es igual al valor de la función en ese punto.
Si alguna de estas igualdades no se cumple, la función no es continua en el punto , y el punto se llama punto de discontinuidad.
En esta denominación, podemos ir un paso más allá y distinguir entre tipos de puntos de discontinuidad. Lo hacemos de la siguiente manera:
Puntos de discontinuidad de primer tipo
El punto se llama punto de discontinuidad de primer tipo si los límites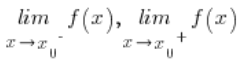 
son finitos (es decir, simplemente números).
Además, si estos límites son iguales entre sí, entonces el punto de discontinuidad de primer tipo se llama removible.
Puntos de discontinuidad de segundo tipo
El punto se llama punto de discontinuidad de segundo tipo si alguno de los límites 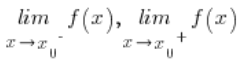no es finito (es decir, simplemente igual a más o menos infinito).
Ejemplo 1
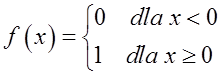
Esta función tiene un punto de discontinuidad en 
(porque el límite por la izquierda en este punto es 0 y el límite por la derecha es 1). Es un punto de discontinuidad de primer tipo porque los límites por la izquierda y por la derecha en este punto son finitos (0 y 1). No es un punto de discontinuidad de primer tipo removible porque los límites no son iguales.
Ejemplo 2
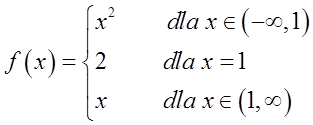
Esta función tiene un punto de discontinuidad en 
(porque los límites por la izquierda y por la derecha en este punto no son iguales al valor de la función en este punto). Es un punto de discontinuidad de primer tipo porque los límites por la izquierda y por la derecha son finitos (e iguales a 1). Es un punto de discontinuidad de primer tipo removible porque los límites por la izquierda y por la derecha son iguales.
Ejemplo 3
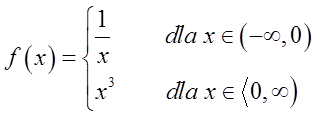
Esta función tiene un punto de discontinuidad en (porque los límites por la izquierda y por la derecha en este punto no son iguales). Es un punto de discontinuidad de segundo tipo porque el límite por la izquierda en este punto es 
.
