Tenemos el límite de una función:
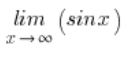
Intuitivamente sentimos que el límite anterior no existe. Los valores de x son cada vez más grandes, y los valores del seno «oscilan» todo el tiempo entre -1 y 1.
Demostración formal
¿Pero cómo demostrar esto formalmente?
De la definición de límite de una función cuando x tiende a infinito, sabemos que el límite existe si para cada secuencia de argumentos de la función que diverge a 
la correspondiente secuencia de valores de la función converge al mismo número (entonces ese número es el límite).
Para mostrar que dicho límite no existe, basta con tomar dos secuencias cualesquiera de argumentos que divergen a y mostrar que las correspondientes secuencias de valores convergen a dos números diferentes.
Sabemos que la función seno es periódica, por lo que estas secuencias pueden ser, por ejemplo:
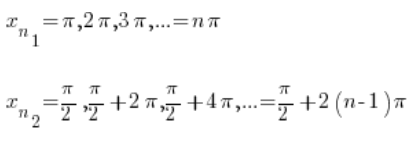
Obviamente, ambas secuencias divergen al infinito cuando 
.
Ahora miremos las secuencias de valores de la función correspondientes a estas secuencias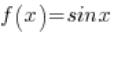 
:
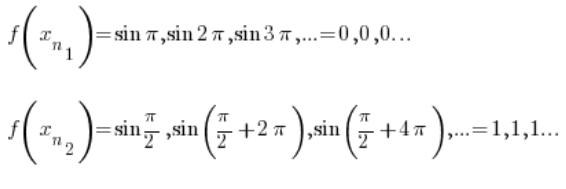
Obviamente, la primera secuencia converge a 0, y la segunda secuencia converge a 1.
Esto es suficiente para demostrar que el límite de la función:
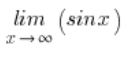
no existe.
