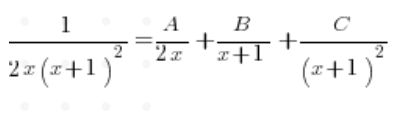Delta igual a cero en integrales racionales indefinidas
Krystian Karczyński
Fundador y jefe del servicio eTrapez.
Maestro en Matemáticas por la Universidad Tecnológica de Poznań (Polonia). Tutor de matemáticas con muchos años de experiencia. Creador de los primeros Cursos eTrapez, que se han vuelto enormemente populares entre estudiantes de toda Polonia.
Vive en Szczecin (Polonia). Le gusta caminar por el bosque, ir a la playa y hacer kayak.
Descomposición de un trinomio cuadrático
En integrales racionales indefinidas, a menudo es necesario descomponer un trinomio cuadrático: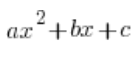 
. Lo hacemos por supuesto con la fórmula: 
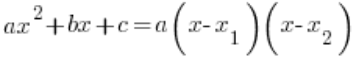, que funciona cuando 
.
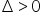Integrales racionales y delta igual a 0
Pero, ¿cómo se ve este binomio cuando Delta es exactamente 0? Por ejemplo, ¿cómo se ve la descomposición en factores: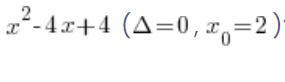 
?
¿Será así: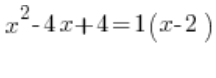 
?
Claro que no… Desde la escuela secundaria recordamos que si 
, obtenemos una raíz, pero es una doble raíz. Entonces, en nuestro ejemplo, podemos decir: 
, lo que significa que el trinomio cuadrático descompuesto en factores se ve así:
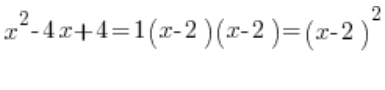
Esto tiene consecuencias significativas para integrales racionales indefinidas al dividirlas en fracciones simples.
Ejemplo
Tomemos un ejemplo:
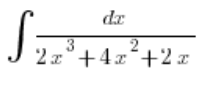
Descomponemos la fracción por sí misma sin la integral, escribiendo:
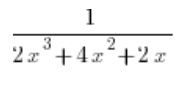
En la parte inferior sacamos x delante del paréntesis:
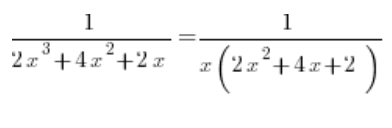
Del trinomio cuadrático en la parte inferior, calculamos la delta, que es 0, y obtenemos la raíz (-1). Así que al descomponerlo en factores obtenemos:
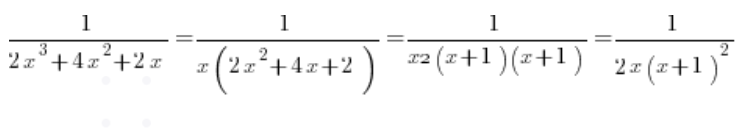
Y al descomponerlo en fracciones simples:
¿Buscas clases particulares de matemáticas para nivel universitario o de secundaria? ¿O quizás necesitas un curso que te prepare para el examen de selectividad?
Somos el equipo de eTrapez. Enseñamos matemáticas de manera clara, sencilla y muy detallada - llegamos incluso al más resistente al aprendizaje.
Hemos creado cursos en video explicados en un lenguaje comprensible para descargar en tu computadora, tableta o teléfono. Enciendes la grabación, miras y escuchas, como en las clases particulares. A cualquier hora del día o de la noche.
