Al calcular raíces cuadradas en forma cartesiana (o: algebraica) en mi Curso de Números Complejos, mostré un método que consiste en añadir una tercera ecuación al sistema ya existente de dos ecuaciones, lo que simplifica y acorta enormemente los cálculos posteriores.
Mostré este método, pero no lo justifiqué de ninguna manera.
Recientemente, recibí un correo electrónico al respecto:
Hola
¿Podría explicar por qué podemos usar el método de añadir una tercera ecuación al calcular la raíz cuadrada de un número complejo?
x^2 + y^2 = el módulo del número cuya raíz estamos calculando
Esta es una pregunta MUY buena y realmente bendecidos en matemáticas son aquellos que no creen ciegamente a los profesores, sino que siempre preguntan: «¿De dónde viene esto?» 🙂
Justificación
Así que no me queda otra opción que justificar este método de una de las posibles maneras:
Después de los primeros pasos en el cálculo de la raíz cuadrada, tenemos la situación:
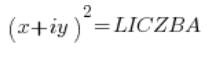
Dado que los números (no voy a escribir «números complejos» cada vez) a la izquierda y a la derecha son iguales, sus módulos también deben ser iguales (no funciona al revés, pero eso no importa), es decir:
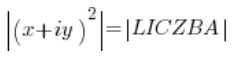
Un número al cuadrado es un número multiplicado por sí mismo, es decir:
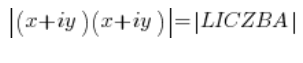
El módulo de un número complejo tiene la propiedad: 
, por lo que en el lado izquierdo podemos escribir:
… y al calcular los módulos a la izquierda tenemos:
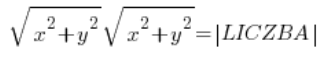
es decir:
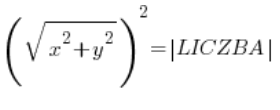
es decir:
es decir:
BINGO
¡Gracias por la buena pregunta!
