Derivando fórmulas para derivadas
Las fórmulas de las derivadas no vienen del espacio exterior, en realidad se derivan de la definición de derivada:
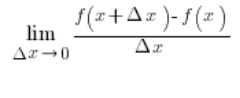
La derivada de la raíz cuadrada de x
Vamos a derivar, por ejemplo, la fórmula para la derivada de la raíz cuadrada de x: 
. Deberíamos obtener: 
(según dicen las fórmulas básicas de derivadas – fórmula número 5).
Tenemos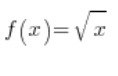 
. A trabajar. Después de sustituir en la fórmula de la derivada de la definición, recibiremos:
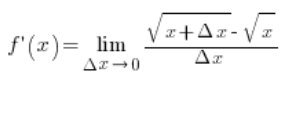
Multiplicando el numerador y el denominador de la siguiente manera…
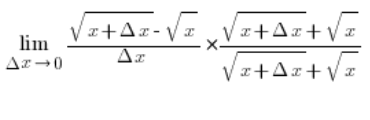
…y utilizando la fórmula del trinomio cuadrado perfecto en el numerador, eliminaremos la irracionalidad y obtendremos:
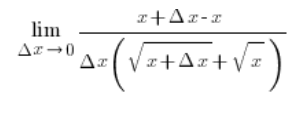
Las x en la parte superior del numerador se cancelarán y obtenemos…
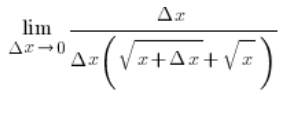
…y después de cancelar 
en el numerador y el denominador:
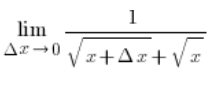
Dado que 
esto significa que:
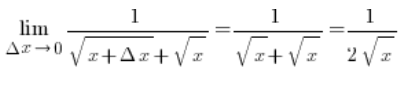
Entonces, estamos en casa. La fórmula para la derivada ha sido derivada.
Más ejemplos
Te animo a que experimentes con otras fórmulas, ¡adelante!
Curso de Derivadas y Análisis del Comportamiento de Funciones
También encontrarás diversos casos calculados paso a paso en mi Curso de Derivadas y Análisis del Comportamiento de Funciones.
Casos más generales
La tarea de derivar una fórmula para una derivada siempre se reduce a calcular el límite adecuado límite, donde ‘x’ se trata como una constante. Puede ser más fácil o más difícil, pero puedes usar métodos y trucos que ya conoces del cálculo de límites de funciones.
Con una salvedad.
Desafortunadamente, la regla de L’Hôpital queda descartada. ¿Por qué? Precisamente porque utiliza derivadas.
Te recuerdo tu tarea: debes calcular la derivada de una función desde la definición, sin conocer la fórmula. Y la regla de L’Hôpital utiliza a menudo fórmulas de derivadas!
