Derivadas Direccionales – ¿Algo Nuevo Otra Vez?

---

Lugar y tiempo de acción

Calcular derivadas direccionales como tema para estudiar (es decir, para aprobar) se sitúa justo después de las derivadas parciales de funciones de varias variables, que la mayoría de los estudiantes cubren en el segundo semestre.

Es un tema tan raramente abordado que no lo incluí en mi Curso sobre derivadas parciales, pero tan común que lo pondré en el blog – para beneficio de aquellos que necesitan aprender derivadas direccionales y aquellos que simplemente tienen curiosidad por saber de qué se trata. Sin embargo, como en los cursos, hoy me concentraré casi exclusivamente en la práctica (“¿cómo lo hago?”), no en la teoría (“¿qué estoy haciendo realmente?”).

Derivadas direccionales – ¿cómo lo hago?

En el caso de la derivada direccional, estamos tratando con el aumento simultáneo de los argumentos x e y, lo que naturalmente corresponde a un cierto aumento en el valor de la función .

Para la tarea, necesitamos tres cosas:

1. Una función de la cual calcularemos la derivada direccional.
2. Un punto en el que calcularemos la derivada direccional.
3. Una dirección dada en forma de vector.

Con lo anterior, la tarea se reduce a convertir el vector en un vector direccional (algo de geometría analítica, mostraré cómo hacerlo en un momento), y luego insertarlo en la fórmula:

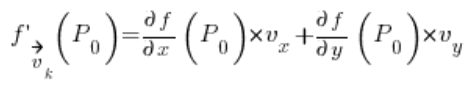
En la cual:

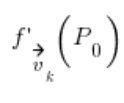es la derivada direccional en el punto en la dirección del vector

es el punto en el cual calculamos la derivada direccional

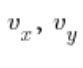son las coordenadas del vector direccional

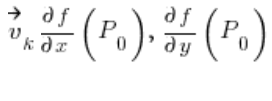son las derivadas parciales de la función en el punto .

Calcula la derivada direccional de la función 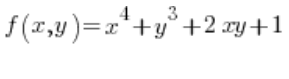en el punto P(1,2) en la dirección .

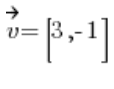Solución:

Todo está listo, solo necesitamos convertir el vector 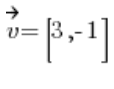en un vector direccional.

Un vector direccional es un vector con la misma dirección (quién lo hubiera pensado), misma orientación, pero con una longitud de 1.

Se calcula por la fórmula:

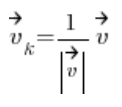
Simplemente, divide sus coordenadas por su longitud.

Entonces calculamos la longitud del vector :

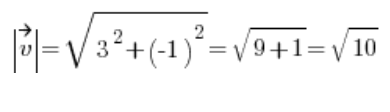
Luego obtenemos el vector direccional:

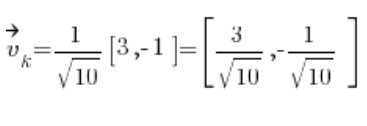
Para la fórmula de la derivada direccional, también necesitamos las derivadas parciales de la función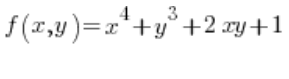 en el punto P(1,2):

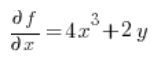
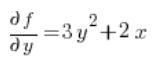
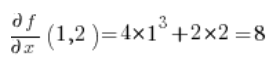
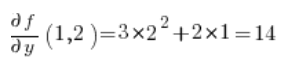
Ahora tenemos todo lo necesario para la fórmula:

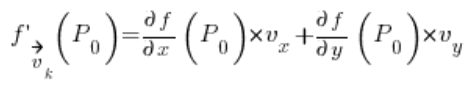
Solo sustituimos y tenemos el resultado: .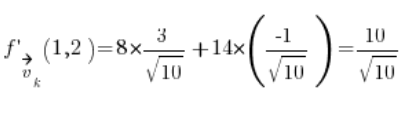

Hecho.

Ejemplo 2

Encuentra la derivada direccional de la función: 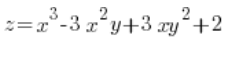en el punto P(3,1) en la dirección desde este punto hasta el punto Q(6,5).

Solución:

La tarea es un poco más difícil porque el vector direccional no está dado directamente, pero no hay problema.

Nos movemos del punto P al punto Q, por lo que el vector de desplazamiento es [3,4].

Ahora buscamos el vector direccional calculando la longitud del vector [3,4]:

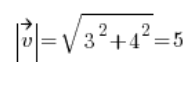
Y tenemos el vector direccional:

Ahora calculamos las derivadas parciales en el punto (3,1):

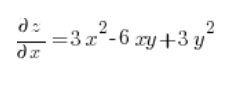
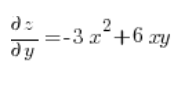
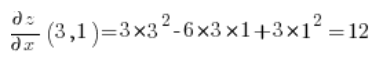
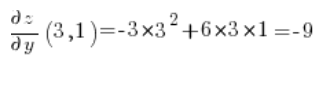
Luego simplemente sustituimos en la fórmula de la derivada direccional:

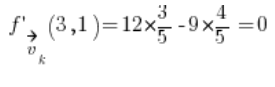
Ejemplo 3

Encuentra la derivada direccional de la función 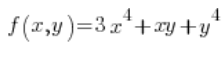en el punto (1,2) en la dirección que forma un ángulo con el eje x positivo.

Solución:

La tarea parece más difícil, debido a la falta de un vector direccional en los datos. Dibujemos toda la cosa:

Se trata de encontrar las coordenadas de cualquier vector en la dirección especificada.

Usamos el hecho de que 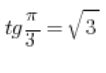y podemos asumir que nuestro vector tiene coordenadas 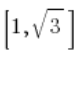, como en el dibujo (era suficiente elegir cualquier vector en la dirección de la línea):

Y ahora procedemos como siempre.

Calculamos el vector direccional:

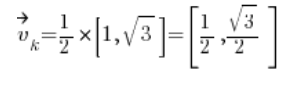
Luego las derivadas parciales en el punto (1,2):

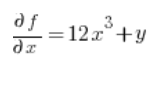
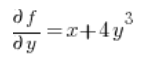
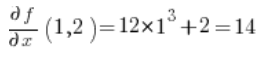
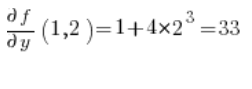
Sustituimos en la fórmula y obtenemos el resultado

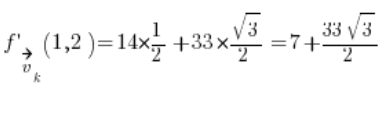
Siéntete libre de hacer preguntas en los comentarios – como siempre 🙂