El volumen de un elipsoide (pero no uno de rotación, sino uno salvaje) calculado por una integral definida
Krystian Karczyński
Fundador y jefe del servicio eTrapez.
Maestro en Matemáticas por la Universidad Tecnológica de Poznań (Polonia). Tutor de matemáticas con muchos años de experiencia. Creador de los primeros Cursos eTrapez, que se han vuelto enormemente populares entre estudiantes de toda Polonia.
Vive en Szczecin (Polonia). Le gusta caminar por el bosque, ir a la playa y hacer kayak.
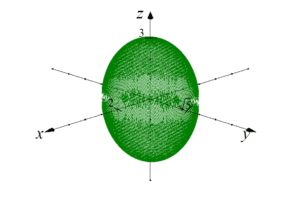
Supongamos que necesitamos calcular el volumen de un elipsoide:
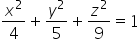
Este es un elipsoide que corta los ejes x, y, z en las coordenadas 2, 
y 3 (la ecuación general del elipsoide es: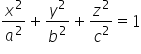 
, donde a, b, c son las coordenadas de intersección).
No es un elipsoide de rotación, no se forma al girar ninguna curva alrededor de ningún eje, por lo que no podemos usar la fórmula estándar para el volumen de un sólido de revolución:
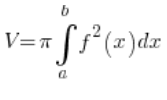
Tenemos que encontrar otra manera.
1. Elegimos cualquier punto M(z) en el centro del elipsoide y en el eje OZ.
El plano que pasa por este punto y es perpendicular al eje OZ “corta” una cierta elipse del elipsoide:
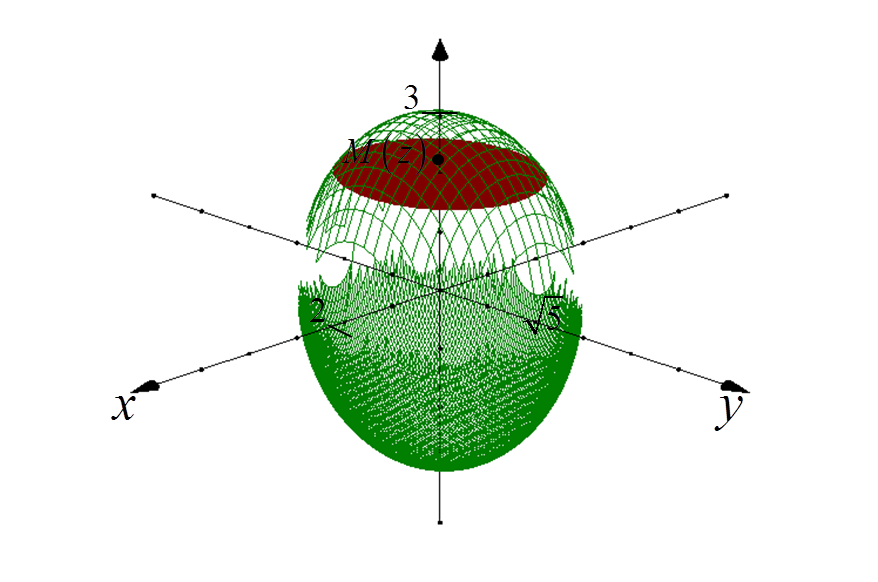
2. Determinamos la ecuación de la proyección de la elipse “cortada” en el plano XY
Determinamos la ecuación de esta elipse, para un ‘z’ fijo (tratamos ‘z’ como una constante) a partir de la ecuación general del elipsoide:
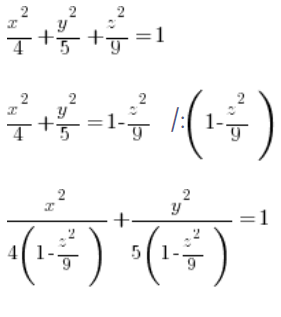
Podemos ver que nuestras ‘a’ y ‘b’ de la ecuación general del elipsoide (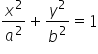
) son:
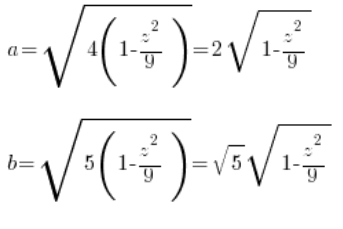
4. Calculamos el área de esta sección en función de la variable ‘z’
El área de esta elipse dependerá del punto ‘z’ elegido, por lo que será una función de la variable ‘z’. Podemos calcularla utilizando la fórmula ya hecha para el área de la elipse (
):
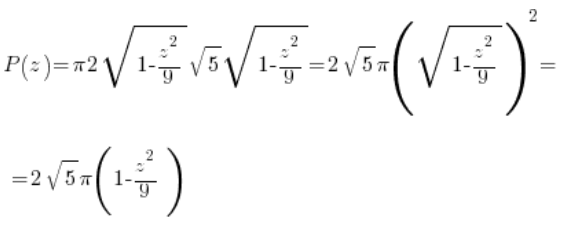
O calculando laboriosamente la integral definida adecuada (utilizando, por supuesto, la forma paramétrica de la elipse y la fórmula para el área de una región en forma paramétrica):
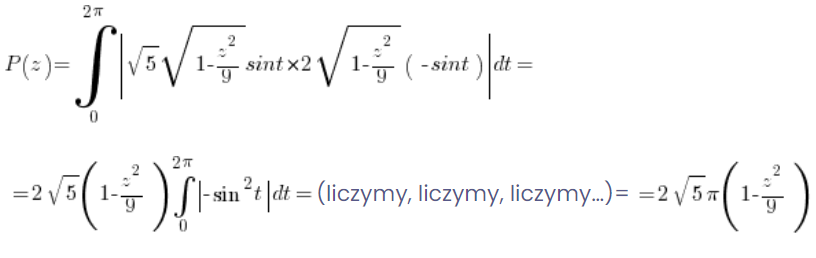
5. Calculamos el volumen del sólido utilizando las áreas de las secciones
Ahora viene la parte difícil. El volumen del sólido es igual – esto suena un poco raro – a la “suma” (es decir, la integral) de todas las secciones, que en general es:
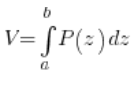
donde 
es la función de las áreas de sección del sólido con un plano perpendicular al eje OZ, y ‘a’ y ‘b’ son los límites en los que varía ‘z’.
Así que para nosotros:
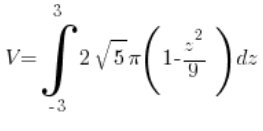= (calculamos, calculamos, calculamos…) = 
Esto coincide con la fórmula general para el elipsoide (
).
FIN
Vale la pena recordar este esquema general y, sobre todo, que el volumen de sólidos más complejos, no rotacionales, se puede calcular integrando la función de sus áreas de sección.
¿Buscas clases particulares de matemáticas para nivel universitario o de secundaria? ¿O quizás necesitas un curso que te prepare para el examen de selectividad?
Somos el equipo de eTrapez. Enseñamos matemáticas de manera clara, sencilla y muy detallada - llegamos incluso al más resistente al aprendizaje.
Hemos creado cursos en video explicados en un lenguaje comprensible para descargar en tu computadora, tableta o teléfono. Enciendes la grabación, miras y escuchas, como en las clases particulares. A cualquier hora del día o de la noche.
