Esta publicación es ya la tercera consecutiva en la que quiero llamar tu atención sobre cosas que vale la pena repasar al comienzo de tus estudios de matemáticas en la universidad. Una rápida revisión de ellos te facilitará mucho la vida en la universidad. En publicaciones anteriores, traté los temas de:
Interpretación geométrica del valor absoluto
Hoy le toca al función cuadrática.
¿Función cuadrática? Pero creo que estuvimos dos meses con eso…
El tema de la función cuadrática es, por supuesto, muy amplio y no me refiero en absoluto a que tomes un libro de texto de la escuela secundaria y repases todo el capítulo de principio a fin.
Centrámonos solo en algunos detalles importantes, matices y trampas.
Función cuadrática vs. ecuación cuadrática
Función cuadrática es, por supuesto, algo como esto:
![]() o:
o: 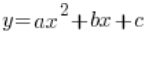
Donde ![]() son números cualesquiera. Ejemplos de funciones cuadráticas son:
son números cualesquiera. Ejemplos de funciones cuadráticas son:
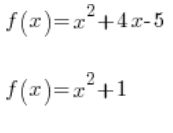
y así…
El concepto de función cuadrática debe diferenciarse del concepto de ecuación cuadrática, por ejemplo:
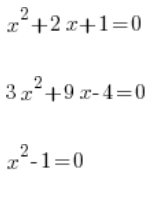
y así…
¡¡¡No es lo mismo!!!!
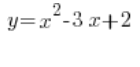 es una función cuadrática, mientras que
es una función cuadrática, mientras que 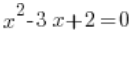 es una ecuación cuadrática.
es una ecuación cuadrática.
No distinguir entre función y ecuación a menudo lleva a…
Error macabro número 1
Al calcular, por ejemplo, derivadas y tener una función dada:
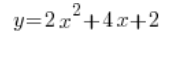
Las personas a menudo hacen algo como esto:
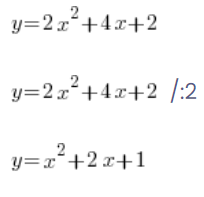
…y siguen calculando lo que sea necesario.
Se equivocan porque recuerdan que podían hacer algo similar con ecuaciones:
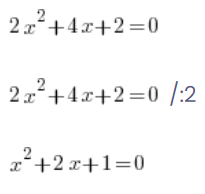
…y con ecuaciones, todo está bien, puedes dividir ambos lados, 0 en el lado derecho dividido por 2 realmente da 0 y las ecuaciones son equivalentes (tienen las mismas soluciones).
Pero no puedes hacer esto con funciones – tendrías que dividir también ese y en el lado izquierdo, etc. ¡Al dividir simplemente el valor de la función por 2, obtendrás una función diferente!
¿Qué necesitas repasar de las funciones?
No mucho. En realidad, solo dos formas de la función: canónica y factorizada.
La forma canónica de la función cuadrática
Asumo que ya tenemos la forma general de la función cuadrática:
![]()
Su forma canónica es:
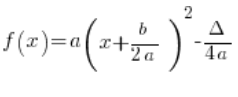
Es decir:
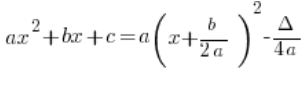
Qué son a, b y ![]() se sabe, pocas personas tienen problemas con
se sabe, pocas personas tienen problemas con ![]() .
.
Incluso se puede notar que si factorizamos ![]() en la forma canónica, obtendremos:
en la forma canónica, obtendremos:
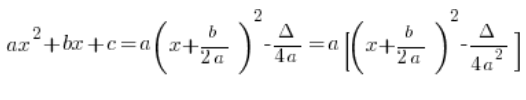
…lo que a veces puede ser útil y a veces no necesariamente.
Si aprendiste esto calculando las coordenadas del vértice (generalmente como ![]() y
y ![]() ) e insertándolas en la fórmula:
) e insertándolas en la fórmula:
![]() entonces, por supuesto, es un poco indirecto, pero también genial.
entonces, por supuesto, es un poco indirecto, pero también genial.
¡Recuerda ![]() al comienzo de la forma canónica!
al comienzo de la forma canónica!
La forma factorizada de la función cuadrática (su factorización):
Volviendo ahora a nuestra función cuadrática general:
![]()
A menudo necesitaremos «factorizarla», usando la forma factorizada de la función cuadrática:
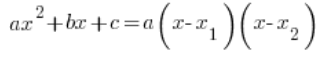
Donde ![]() y
y ![]() se calculan a partir de las fórmulas conocidas y queridas:
se calculan a partir de las fórmulas conocidas y queridas:
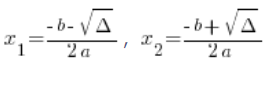
Aquí también debes recordar ![]() al comienzo de la fórmula!!!
al comienzo de la fórmula!!!
También nota que estos ![]() y
y ![]() no siempre existen (si Δ es negativo, no existen), lo que significa que la función no siempre se puede escribir en forma factorizada, es decir, una función cuadrática no siempre se puede factorizar.
no siempre existen (si Δ es negativo, no existen), lo que significa que la función no siempre se puede escribir en forma factorizada, es decir, una función cuadrática no siempre se puede factorizar.
¿Qué necesitas repasar de las ecuaciones cuadráticas?
Con las ecuaciones cuadráticas, supongo que las cosas no están tan mal. Por lo general, podemos resolver la ecuación general:
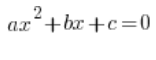
Por ejemplo:
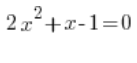
Simplemente calculamos:
![]()
Luego, si Δ es no negativo, soluciones de la ecuación:
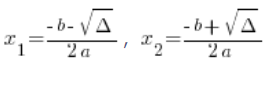
Recuerda que en el denominador hay ![]() y no simplemente 2!
y no simplemente 2!
Sin embargo, me gustaría detenerme en un caso particular de la ecuación:
![]()
Aquí ocurren muchos errores. Por ejemplo:
Error macabro número 2
![]()
![]()
¿Cuál es el error exactamente? El número 2 es, de hecho, una solución de la ecuación ![]() , pero se omitió por completo la segunda solución de esta ecuación, a saber, el número -2. Debería ser:
, pero se omitió por completo la segunda solución de esta ecuación, a saber, el número -2. Debería ser:
![]()
![]()
Las soluciones negativas solo se pueden ignorar en geometría (porque la distancia no puede ser negativa).
Otro problema con la ecuación en la forma: ![]() es:
es:
Error macabro número 3
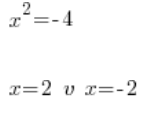
Lo cual es, por supuesto, una tontería, porque 2 al cuadrado no da -4. De hecho, nada al cuadrado da -4 (aquellos que ya han estudiado números complejos, manténganse en silencio). La ecuación:
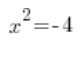
…no tiene soluciones.
Así que debes estar alerta. La ecuación ![]() tiene dos soluciones y la ecuación
tiene dos soluciones y la ecuación ![]() no tiene ninguna solución.
no tiene ninguna solución.
Te invito a repasar tranquilamente todo lo dicho hasta ahora y, por supuesto, a hacer preguntas en los comentarios.


