La relación entre las asíntotas horizontales y oblicuas es la siguiente: las asíntotas horizontales son un caso especial de las asíntotas oblicuas. Por lo tanto, toda asíntota horizontal es también oblicua, pero no toda oblicua es horizontal.
Puedes y deberías utilizar esto para facilitarte el cálculo de las asíntotas de una función. Hay básicamente dos enfoques para este tema:
1. Primero, calculamos las asíntotas horizontales
Este enfoque se muestra en mi Curso de Video sobre el estudio del comportamiento de las funciones.
La condición para que una función tenga una asíntota horizontal es:
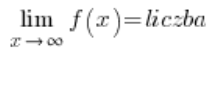 o
o 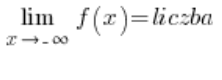
Si aparecen asíntotas horizontales, ya no calculamos las oblicuas (como si las oblicuas ya se hubieran determinado – recuerda que las horizontales son un tipo de oblicuas). Sin embargo, si no aparecen asíntotas horizontales, entonces tenemos un problema – debemos recalcular las asíntotas oblicuas.
Por supuesto, la situación es un poco más complicada: una asíntota horizontal podría «aparecer» en ![]() , y «no aparecer» en
, y «no aparecer» en ![]() . En tales casos, no investigaríamos la existencia de una asíntota oblicua en
. En tales casos, no investigaríamos la existencia de una asíntota oblicua en ![]() (ya que ya apareció allí), pero necesitaríamos comprobar su presencia en
(ya que ya apareció allí), pero necesitaríamos comprobar su presencia en ![]() .
.
2. Primero calculamos las asíntotas oblicuas
…y luego las asíntotas horizontales aparecerán (o no) automáticamente; solo necesitamos interpretar correctamente los resultados. Este enfoque no se muestra en mi curso. El inconveniente es que las condiciones para la existencia de una asíntota oblicua de una función son un poco más complicadas:
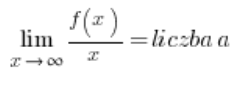 y
y 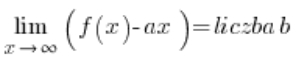
o:
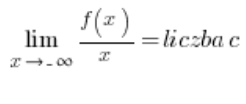 y
y 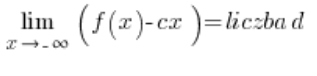
…y la ventaja es que una vez calculadas, no hay necesidad de calcular más. Si las condiciones se cumplen y el número ![]() (o
(o ![]() ) de las condiciones para la existencia de una asíntota oblicua resulta ser igual a
) de las condiciones para la existencia de una asíntota oblicua resulta ser igual a ![]() , significa que la asíntota oblicua es realmente una asíntota horizontal.
, significa que la asíntota oblicua es realmente una asíntota horizontal.
Para simplificar aún más el trabajo, podemos calcular directamente:
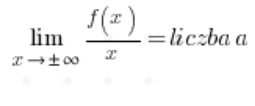 y
y 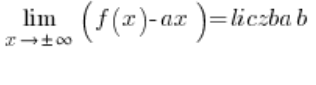
Y solo separamos el cálculo de las condiciones para ![]() y
y ![]() cuando sea necesario (cuando haga una diferencia en el resultado si �
cuando sea necesario (cuando haga una diferencia en el resultado si �
x tiende hacia ![]() o hacia
o hacia ![]() ).
).