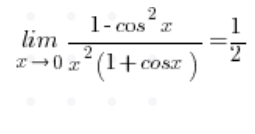We usually treat the limits of a sine function as: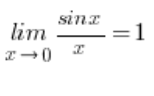
(you can find the derivation of this formula here ).
Question: what about cosine of x?
Formula for the limit of a function with cosine
Of course, this does not happen: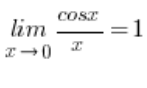
, because the limit of the function
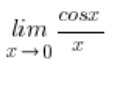it is not an unmarked symbol at all.
For limits on the cosine of x, the formula is often helpful:
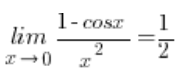– in many textbooks it is already given “at the beginning”, without any demonstration, and in many textbooks it is given as a limit of a function that needs to be calculated.
Regardless of your case, it is worth knowing how to derive this formula, and it goes like this:
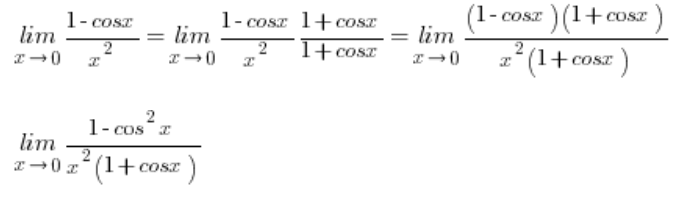
At this point, I use trigonometric one in the numerator:
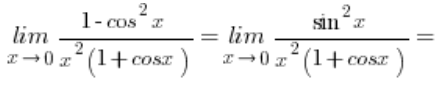
The limit of the function z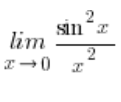
runs down to
, because:
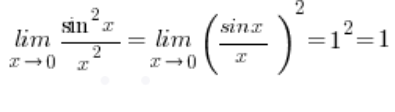
And the limit of the function z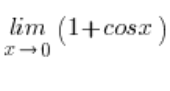
runs down to
, because
, so we have the result:
