Continuity of functions at a point
As we all know, function
is continuous at a point 
, When:
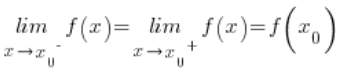
That is, whenthe limit of this function from below at this point is equal to the limit of the function from above at this point is equal to the value of the function at this point.
If any of the equality is not satisfied, the function is discontinuous at a point , and the point is called the discontinuity .
In this naming, you can go a step further and DISTINGUISH the discontinuities. We do it like this:
Discontinuity of the first type
Discontinuity we call it discontinuity of type I if the limits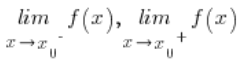 
are finite (i.e. they are simply numbers).
Additionally, if these limits are equal, then the point of discontinuity of type I is called removable .
Points of discontinuity of the second type
Discontinuity we call a type II discontinuity if some of the limits 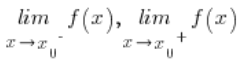is not finite (i.e. it simply equals infinity plus or minus).
Example 1
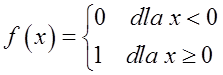
This function has a point 
discontinuity (because the below boundary at this point is 0 and the above boundary is 1 ). This is discontinuity of the first type, because the below and above limits at this point are finite (0 and 1). However this is not a removable discontinuity, because the limits are not equal.
Example 2
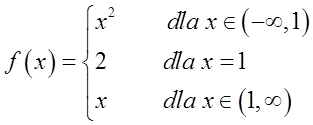
This function has a point 
discontinuity (because the below and above limits at this point are not equal to the value of the function at this point). This is a discontinuity of the first type, because the below and above limits are finite (and equal to 1). This is a removable discontinuity of the first type, because the below and above limits are equal.
Example 3
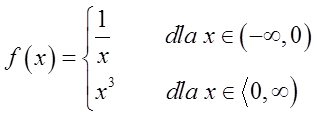
This function has a point discontinuity (because the below and above limits at this point are not equal). This is a point of type II discontinuity, because the below limit at this point is equal
.
