When solving problems with complex numbers, it’s important to remember that a complex number in trigonometric form looks like this:
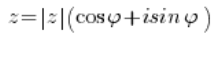
And only like this. No more, no less.
So, you need to pay attention to:
When is a complex number in trigonometric form and when is it not?
- The number:
IS in trigonometric form, where the modulus of the number is equal to 1 (), because of course:
- The number: is NOT in trigonometric form because before the imaginary unit ‘i’ multiplied by sine there is a minus sign, but it should be a plus sign.
To convert this number to trigonometric form, we need to use trigonometric formulas:
Using these formulas, we can convert:
Sine and cosine functions are-periodic, so their value is the same as . I wrote more about this in: this post.
So in the end, we have:
…and this is a number in trigonometric form. - The number: is NOT in trigonometric form because before the imaginary unit ‘i’ multiplied by sine there is a minus sign, but it should be a plus sign, and before the cosine there is a minus sign, but it should be a plus sign.
To convert this complex number to trigonometric form, we need to factor out the minus sign in front of the parentheses:
Convert the number to trigonometric form (we already know how to do this…):
So we have the multiplication of two numbers in trigonometric form:
To multiply numbers in trigonometric form, we multiply their moduli and add their arguments (there’s a formula for this), so we have:
And this is a number in trigonometric form. - The number: is NOT a complex number in trigonometric form because there is a minus sign before the cosine, but it should be a plus sign.
To convert this complex number to trigonometric form, you need to factor out the minus sign in front of the parentheses:
The number -1 needs to be converted to trigonometric form (we did this in point 3), similarly, the number needs to be converted to trigonometric form (we did this in point 2).
We get:
Using the formula for multiplying trigonometric functions:
And using the periodicity of the sine and cosine functions:
- The number: is NOT a complex number in trigonometric form because there is an imaginary unit ‘i’ before the cosine (and it shouldn’t be there), and there is no imaginary unit ‘i’ before the sine.
You need to use the trigonometric formulas known from high school:
So we have:
And this is a complex number in trigonometric form. - The number: is NOT a complex number in trigonometric form.
You need to swap the sine and cosine just like we did in point 5, and then solve it like we did in point 4. - The number: is NOT a complex number in trigonometric form.
You need to swap the sine and cosine just like we did in point 5, and then solve it like we did in point 2. - The number: is NOT a complex number in trigonometric form.
You need to swap the sine and cosine just like we did in point 5, and then solve it like we did in point 3.
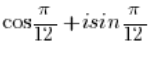IS in trigonometric form, where the modulus of the number is equal to 1 (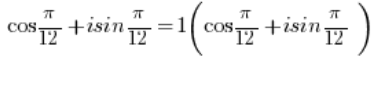
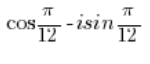), because of course:
is NOT in trigonometric form because before the imaginary unit ‘i’ multiplied by sine there is a minus sign, but it should be a plus sign.
-periodic, so their value is the same as 
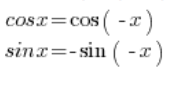
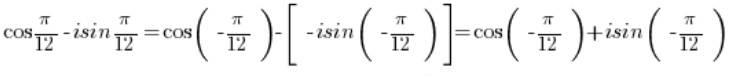
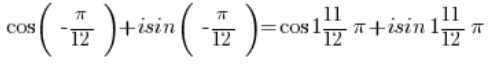
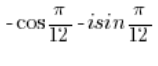is NOT in trigonometric form because before the imaginary unit ‘i’ multiplied by sine there is a minus sign, but it should be a plus sign, and before the cosine there is a minus sign, but it should be a plus sign.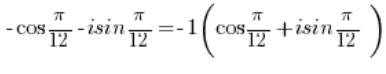
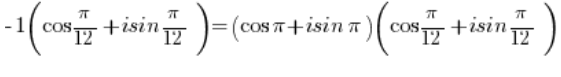
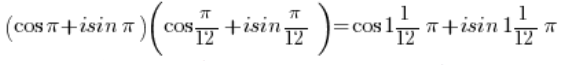
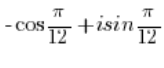to trigonometric form (we already know how to do this…):
is NOT a complex number in trigonometric form because there is a minus sign before the cosine, but it should be a plus sign.
needs to be converted to trigonometric form (we did this in point 2).
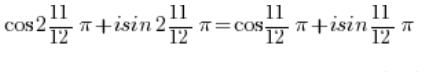
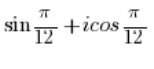is NOT a complex number in trigonometric form because there is an imaginary unit ‘i’ before the cosine (and it shouldn’t be there), and there is no imaginary unit ‘i’ before the sine.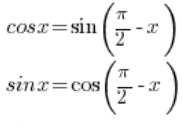
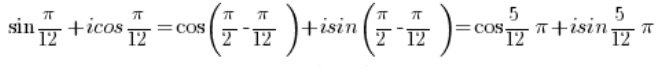
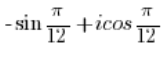is NOT a complex number in trigonometric form.
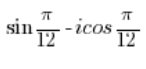is NOT a complex number in trigonometric form.
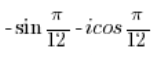is NOT a complex number in trigonometric form.Good luck! 🙂
