Calculate the parameter ‘a’ in the above system of equations, knowing that it is inconsistent.
Instead of systematically starting by calculating the rank of the main matrix, let’s determine the rank of the augmented matrix:
…it is equal to two because in this matrix you can extract a non-zero second-order determinant (and you can’t get a larger one):
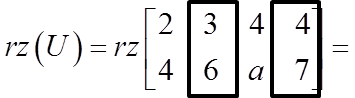
So the rank of the augmented matrix is 2.
Applying the Kronecker-Capelli Theorem
So what should the rank of the main matrix be?
We know that the system is inconsistent, and from the Kronecker-Capelli Theorem we know that it will be inconsistent when the rank of the main matrix is different from the rank of the augmented matrix. We also know that the rank of the main matrix is always less than or equal to the rank of the augmented matrix (the main matrix is contained within the augmented matrix). So the rank of the main matrix should be 1 or 0 (to be different from the rank of the augmented matrix).
The rank of the main matrix will be:
We see that it definitely won’t be 0 (only the zero matrix has a rank of 0) – so it should be 1. The rank will be one when the first and second rows are proportional (then we will remove one of them). We see that the first row multiplied by two gives the second row, if only a equals 8.
So quickly and without big calculations we come to the answer:
