Limit of the Function: x to the x to the x … What to Do? (Example with Morals)
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
As a curiosity, I’ll calculate the limit of the function:
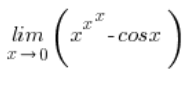
More interesting than the calculations themselves are the two morals that can be drawn from them. But the morals are at the end (has anyone ever seen a story with a moral at the beginning)? Now, I’m calculating:
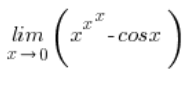
At the beginning, I look at what the expression approaches, and I get:
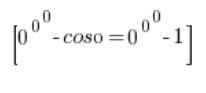
So, I have no idea what it approaches because I don’t even know what 
approaches (this is an indeterminate form), let alone something weird like: 
.
However, it looks like there are no problems with the cosine, so I calculate on the side what this approaches:
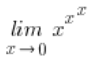
I will use the approach of L’Hôpital (I showed exactly what this is about in my Course), which means I’ll use the formula (
):
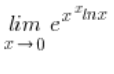
But it’s still not great, because I still have an indeterminate form in the exponent 
, so I transform it a second time:
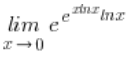
Now I can calmly get to work. I calculate on the side:
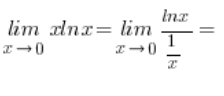
, so I have an indeterminate form 
so I use L’Hôpital’s rule:
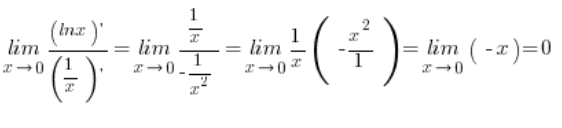
So, I’ve calculated on the side that: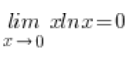 
.
Returning to the limit:
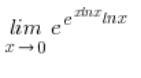
I now know that I’m in the situation:
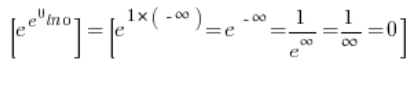
So it turns out that:
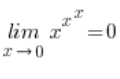
So, my whole limit is:
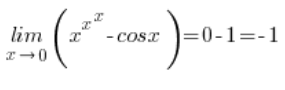
And the cosine was just for show.
Morals of this story
There are two.
- In harder limits, you can always and sometimes need to take a part of it and calculate what it approaches “on the side”.
- Sometimes, some parts of the limit formula can be added in like this cosine. It turned out that I didn’t have to do anything with it, just substitute zero at the end.
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.
